Isosceles Triangle with Two Points on Base
What Is This About?
Problem
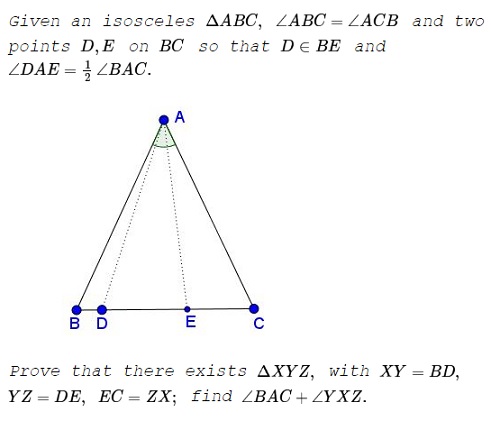
Solution 1
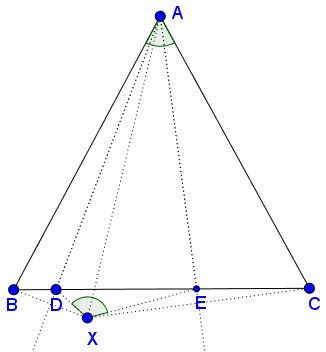
Reflect $B\,$ in $AD\,$ to obtain point, say, $B'.\,$ Note that $\Delta BAB'\,$ is isosceles, with $AB=AB'\,$ and $\angle BAB'=2\angle DAB'=2\angle DAB.\,$
SImilarly, if we reflect $C\,$ in $AE\,$ to obtain point, say, $C',\,$ we'll have $\Delta CAC'\,$ isosceles, with $AC=AC'\,$ and $\angle CAC'=2\angle EAC'=2\angle CAE.\,$
Since
$\angle BAB'+\angle CAC'=2(\angle DAB+\angle CAE)=2\angle DAE=\angle BAC,$
implying that the lines $AB'\,$ and $AC'\,$ coincide and, since $AB'=AB=AC=AC',\,$ $B'=C'.\,$ We may as well denote this point as $X\,$ because $\Delta DXE\,$ is the required triangle, with $Y=D\,$ and $E=Z.$
Concerning the angles, $\angle AXD=\angle ABD=\frac{1}{2}(180^{\circ}-\angle BAC).$ The same holds for $\angle AXE=\frac{1}{2}(180^{\circ}-\angle BAC),\,$ implying
$\angle DXE=\angle AXD+\angle AXE'=180^{\circ}-\angle BAC,$
so that $\angle DXE+\angle BAC=180^{\circ}.$
Solution 2
Let $F\,$ in $DE\,$ be such that $BAD = DAF;\,$ $G\,$ is the intersection of the circumcircle $(ABC)\,$ and $AF.\,$ We have $\displaystyle\frac{BD}{DF} = \frac{AB}{AF} = \frac{AC}{AF} = \frac{CE}{EF},\,$ from which
$\displaystyle\frac{BG}{GC} = \frac{BF}{FC} = \frac{BD}{EC}$
and
$\displaystyle\frac{FD}{FB} = \frac{FE}{FC} = \frac{DE}{BC}$
and the conclusion follows.
Solution 3
Let $\angle BAC = 2\theta.\,$ Let us drop a perpendicular from $A\,$ to $BC\,$ intersecting $BC\,$ at $O.\,$ Let $l(AO)=h.\,$ Let $\angle DAO = \phi.\,$ Note: it is not possible to have both points $D\,$ and $E\,$ to the same side of $O\,$ because $\angle DAE = \theta.\,$ Thus, $\angle EAO = \theta-\phi.\,$ Also, $\angle BAD = \theta-\phi\,$ and $\angle CAE=\phi.\,$ Let $l(XY)=z,\,$ $l(YZ)=x,\,$ and $l(XZ)=y.\,$ Thus,
$\begin{align} x&= h\tan\phi+h\tan(\theta-\phi) \\ y&= h\tan\theta-h\tan(\theta-\phi) \\ z&= h\tan\theta-h\tan\phi \end{align}$
Note that bothe $\phi\,$ and $\theta\,$ are acute angles with $\theta\ge \phi.\,$ Thus,
$\begin{align} x+y&= h\tan\phi+h\tan\theta\ge h\tan\theta-h\tan\phi=z, \\ x+z&= h\tan(\theta-\phi)+h\tan\theta\ge h\tan\theta-h\tan(\theta-\phi)=y, \\ y+z&= [h\tan\theta-h\tan(\theta-\phi)]+[h\tan\theta-h\tan\phi] \\ &\ge h\left[\frac{\tan\theta-\tan(\theta-\phi)}{1+\tan\theta\tan(\theta-\phi)}\right]+h\left[\frac{\tan\theta-\tan\phi}{1+\tan\theta\tan\phi}\right] \\ &= h\tan\phi+h\tan(\theta-\phi) =x. \end{align}$
Thus, the converse of the triangle inequality theorem guarantees the existence of a triangle with $x,\,$ $y,\,$ and $z$ as sides. The existence of two points $D\,$ and $E\,$ distinct from $B\,$ and $C\,$ implies that neither $\phi=0\,$ nor $\theta-\phi=0.\,$ Applying the Cosine rule to the triangle,
$\begin{align} \cos\angle YXZ&= \frac{y^2+z^2-x^2}{2yz} \\ &= \frac{[\tan\theta-\tan(\theta-\phi)]^2+[\tan\theta-\tan\phi]^2-[\tan\phi+\tan(\theta-\phi)]^2}{2[\tan\theta-\tan(\theta-\phi)][\tan\theta-\tan\phi]} \\ &= \frac{\tan^2\theta-\tan\theta\tan\phi-\tan\theta\tan(\theta-\phi)-\tan\phi\tan(\theta-\phi)}{\tan^2\theta-\tan\theta\tan\phi-\tan\theta\tan(\theta-\phi)+\tan\phi\tan(\theta-\phi)} \\ &= \frac{\tan\theta[\tan(\theta-\phi)(1+\tan\theta\tan\phi)]-\tan(\theta-\phi)[\tan\theta+\tan\phi]}{\tan\theta[\tan(\theta-\phi)(1+\tan\theta\tan\phi)]-\tan(\theta-\phi)[\tan\theta-\tan\phi]} \\ &= \frac{\tan(\theta-\phi)\tan\phi(\tan^2\theta-1)}{\tan(\theta-\phi)\tan\phi(\tan^2\theta+1)} \\ &= -(\cos^2\theta-\sin^2\theta) = -\cos 2\theta = \cos(\pi-2\theta). \end{align}$
Thus, $\angle BAC + \angle YXZ = 180^o.\,$
Acknowledgment
The problem has been kindly posted by Leo Guigiuc at the CutTheKnotMath facebook page. The problem has been originally offered at a 2014 high-school olympiad. Solution is by Rachid El Moussaoui; Solution 2 is by a Vietnamese citizen who signs in Kanji; Solution 3 is by Amit Itagi.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574510
