Isogonal Concurrencies
What is this about?
Acknowledgment
The applet above illustrates four distinct concurrencies associated with the triangle formed by isogonally conjugate cevians. The first three have been dealt with early on at Morley's triangle discussion and a separate page. The fourth one has been brought to my attention by Daniel Hardisky who posted the result and a proof at the CutTheKnotMath facebook page.
Below I give a simplified version of the proof.
Problem
Let in $\Delta ABC$ the pairs of lines $AE,AG;$ $BE,BF;$ $CF,CG$ be isogonal conjugate with respect to angles $BAC, CBA, ACB.$ Let $A',B',C'$ be the projections of $F,G,E$ on the sides $BC,AC,AB,$ respectively.
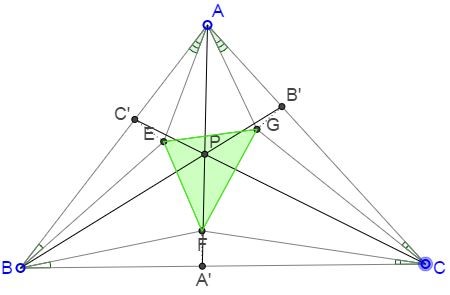
Then lines $AA',BB',CC'$ are concurrent.
Proof
The proof is elementary and depends on the inverse of Ceva's Theorem.
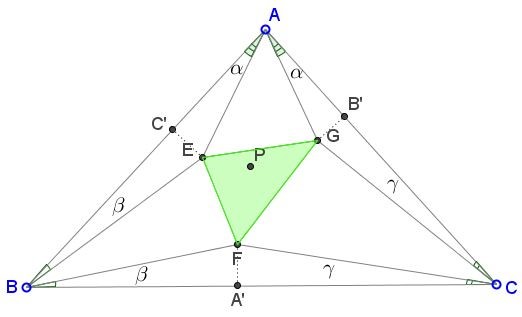
Let $\angle C'AE=\angle B'AG=\alpha,$ $\angle C'BE=\angle A'BF=\beta,$ $\angle A'CF=\angle B'CG=\gamma,$ $FA'=m.$ Then $BA'=m\cdot\cot\beta,$ $CA'=m\cdot\cot\gamma$ so that
$\displaystyle\frac{CA'}{BA'}=\frac{\cot\beta}{\cot\gamma}.$
Similarly,
$\begin{align}\displaystyle \frac{CB'}{AB'} &=\frac{\cot\gamma}{\cot\alpha},\\ \frac{AC'}{BC'} &=\frac{\cot\alpha}{\cot\beta} \end{align}$
Multiplying the three yields Ceva's condition $\displaystyle\frac{CA'}{BA'}\cdot\frac{CB'}{AB'}\cdot\frac{AC'}{BC'}=1$ which exactly says that $AA',BB'CC'$ are concurrent.
![]()
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1966-2016 Alexander Bogomolny73580665
