Projections of Isogonal Conjugate are Concyclic
What Might This Be About?
Problem
In $\Delta ABC$ points $P$ and $Q$ are isogonal conjugates. $\Delta P_{a}P_{b}P_{c}$ and $\Delta Q_{a}Q_{b}Q_{c}$ are the pedal triangles of $P$ and $Q,$ respectively.
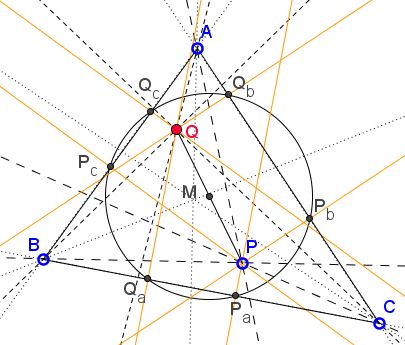
Then points $P_a,$ $P_b,$ $P_c,$ $Q_a,$ $Q_b,$ $Q_c$ are concyclic. The center $M$ of the common circumcircle of $\Delta P_{a}P_{b}P_{c}$ and $\Delta Q_{a}Q_{b}Q_{c}$ is the midpoint of $PQ.$
Solution
As we know, $P_{b}P_{c}\perp AQ.$
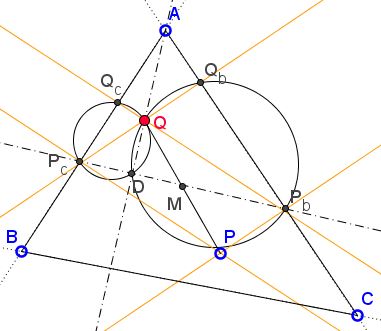
This implies that, if $D$ is the intersection of $P_{b}P_{c}$ and $AQ,$ the quadrilaterals $QQ_{c}P_{c}D$ and $QQ_{b}P_{b}D$ are cyclic; therefore
$AQ_{b}\cdot AP_{b} = AQ\cdot AD = AQ_{c}\cdot AP_{c},$
which in turn means that the four points $Q_{b},$ $P_{b},$ $Q_{c},$ $P_{c}$ are concyclic. The center of their circumcircle lies at the intersection of the perpendicular bisectors of $P_{b}Q_{b}$ and $P_{c}Q_{c}.$ But, since the four points are the projections of $P$ and $Q,$ the bisectors meet at the midpoint $M$ of $PQ.$ The same obviously holds for the other two pairs of points. The three circles thus obtained share the center at two-by-two a pair of points. If so, they coincide.
Note in passing that $D$ is the second points of intersection of circles $(QQ_{c}P_{c}D)$ and $(QQ_{b}P_{b}D)$ and that $QP_{c}$ and $QP_{b}$ are their respective diameters.
In particular case where one of the points $P$ or $Q$ is the centroid of the triangle, the other is its orthocenter, and the common circumcircle of their pedal triangles is none other than the 9-point circle.
Acknowledgment
References
- N. Altshiller-Court, College Geometry, Dover, 1980, pp. 270-271
- R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995, pp. 68-69
- R. A. Johnson, Advanced Euclidean Geometry (Modern Geometry), Dover, 1960, p. 155
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578884
