Concyclic Points in Inscriptible Quadrilateral

What Might This Be About?

24 January 2014, Created with GeoGebra

Problem

In a convex inscriptible quadrilateral $ABCD,$ the perpendicular bisectors of the sides form another inscriptible quadrilateral - $EFGH.$ Let $I$ be the incenter of that quadrilateral.

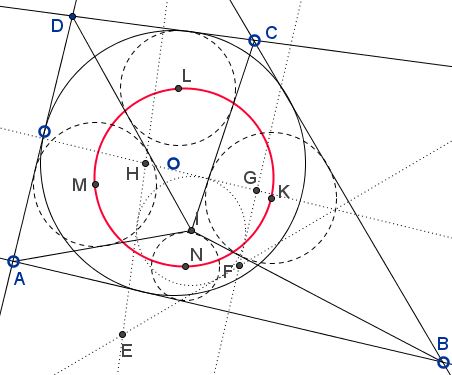
Concyclic Points in Inscriptible Quadrilateral - problem

Then the incenters of triangles $IAB,$ $IBC,$ $ICD,$ $IDA$ are concyclic.

Solution

The fact that $EFGH$ is inscriptible is proved elsewhere. It was discovered by Michael be Villiers several years ago.

Proof of the concyclicity of the incenters is wanting.

Acknowledgment

The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page.

49552162