A Relation in Inscribed Tetrahedra
Source
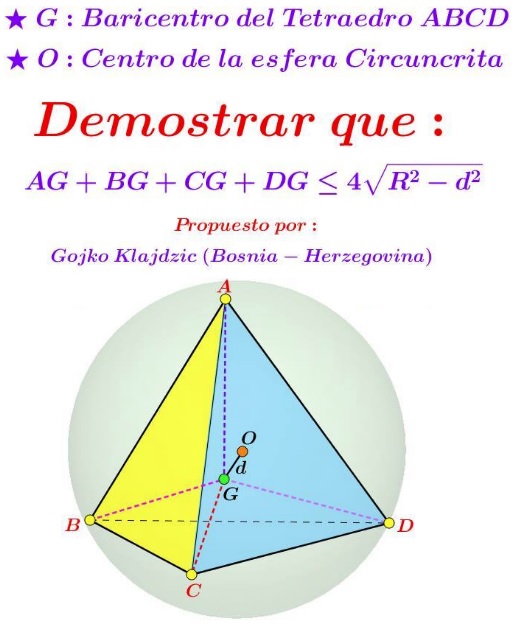
Proof
First, let's evaluate some scalar products, $\overrightarrow{AG}\cdot\overrightarrow{BG},\,$ for example.
On one hand, if the angle between $\overrightarrow{AG}\,$ and $\overrightarrow{BG}\,$ is $\alpha\,$ then $\overrightarrow{AG}\cdot\overrightarrow{BG} = AG\cdot BG\cos\alpha.\,$ On the other hand, $AB^2=AG^2+BG^2-2AG\cdot BG\cos\alpha.\,$ Eliminating $\cos\alpha\,$ from the two expressions shows that $2 \overrightarrow{AG}\cdot\overrightarrow{BG}=AG^2+BG^2-AB^2.$
We have $\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}+\overrightarrow{DG}=\overrightarrow{0},\,$ implying
$(\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}+\overrightarrow{DG})\cdot (\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}+\overrightarrow{DG})=0.$
Let's denote that scalar product as $T.\;$ Then
$\displaystyle\begin{align} T &= \sum_{cycl}AG^2 + 2\sum_{all}\overrightarrow{AG}\cdot\overrightarrow{BG}\\ &=\sum_{cycl}AG^2+\sum_{all}(AG^2+BG^2-AB^2)\\ &= 0 \end{align}$
It follows that $\displaystyle 4\sum_{cycl}AG^2=\sum_{all}AB^2.\,$ On the other hand,
$\overrightarrow{AO}+\overrightarrow{BO}+\overrightarrow{CO}+\overrightarrow{DO}=4\overrightarrow{GO},$
so that $(\overrightarrow{AO}+\overrightarrow{BO}+\overrightarrow{CO}+\overrightarrow{DO})^2=16GO^2\,$ and, subsequently, $16(R^2-d^2)=\displaystyle\sum_{all}AB^2,\,$ i.e.,
$\displaystyle 4\sum_{cycl}AG^2=16(R^2-d^2).$
But $\displaystyle\sum_{cycl}AG\le\sqrt{4\left(\sum_{cycl}AG^2\right)}=4\sqrt{R^2-d^2}.\,$ We are done.
Acknowledgment
The problem has been kindly posted at he CutTheKnotMath facebook page by Leo Giugiuc, along with a solution of his. Leo credits the problem to Gojko Klajdzic (Bosnia-Herzegovina) and Kadir Altintas (Turkey) for passing it along. The graphics is by Miguel Ochoa Sanchez.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573029
