Interpretation of the coordinate formula
for the dot product in 3D
Harry Hirsch
Antwerp, Belgium
Oct 7, 2016
The dot product of two vectors $\overrightarrow{A}(a_1, a_2, a_3)\;$ and $\overrightarrow{B}(b_1, b_2, b_3\;$) which are at an angle $\alpha\;$ is well-known to be $\overrightarrow{A}\cdot\overrightarrow{B} = |\overrightarrow{OA}|\cdot|\overrightarrow{OB}|\cdot\cos\alpha = a_1b_1 + a_2b_2 + a_3b_3,\;$ representing a projection of one vector onto the other.
In a classical proof, one first looks at $|\overrightarrow{B}-\overrightarrow{A}|^2,\;$ which by the Pythagorean theorem is equal to $(b_1-a_1)^2+(b_2-a_2)^2+(b_3-a_3)^2.\;$ After working this out and rearranging, this gives $|\overrightarrow{A}|^2+|\overrightarrow{B}|^2-2(a_1b_1 + a_2b_2 + a_3b_3).\;$ On the other hand, the cosine rule states that $|\overrightarrow{B}-\overrightarrow{A}|^2=|\overrightarrow{A}|^2+|\overrightarrow{B}|^2-2|\overrightarrow{A}||\overrightarrow{B}|\cos\alpha,\;$ giving the result. In another proof, one also includes the fact that the dot product between orthogonal vectors is zero, so that $\overrightarrow{A}\cdot\overrightarrow{B} = (a_1\overrightarrow{x} + a_2\overrightarrow{y} + a_3\overrightarrow{z})∑(b_1\overrightarrow{x} + b_2\overrightarrow{y} + b_3\overrightarrow{z}) = a_1b_1 + a_2b_2 + a_3b_3,\;$ where $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}\;$ are the three unit vectors of the orthogonal basis.
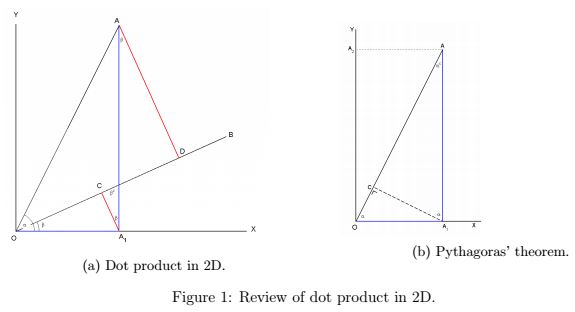
It therefore seems like this coordinate formula is a purely algebraic expression. However one might like to know if there is a geometric interpretation of the coordinate formula, from which one can then prove the projection formula.
Now in 2D, one already has for $\overrightarrow{A}\;$ at angle $\alpha\;$ and $\overrightarrow{B}\;$ at angle $\beta,\;$ both unit vectors, that $\cos (\alpha-\beta ) = \cos\alpha \cos \beta + \sin\alpha\sin\beta.\;$ One can then rescale the equation, by replacing all the terms with the appropriate ratios, e.g. $\cos\alpha =\displaystyle\frac{a_1}{|OA|}\;$ and so on $(|OA|\;$ is the distance (see Figure 1a) between the origin $O,\;$ and point $A:\;$ $|OA|=|\overrightarrow{A}|),\;$ to give the dot product in 2D. Geometrically (Figure 1a), $|OA_1|=\cos\alpha,\;$ and $|A_1A|=\sin\alpha.\;$ Now draw two perpendicular lines from the points $A_1\;$ and $A\;$ onto the line segment $OB.\;$ Then
$|OD| = |OA_1| \cos \beta + |A_1A|\sin \beta = \cos\alpha \cos \beta + \sin\alpha\sin \beta.$
Rescaling gives the desired equation. For Pythagorasí theorem (Figure 1b), we then have
$1 = |OC| + |CA| = |OA_1| \cos\alpha + |A_1A| \sin\alpha = \cos 2\alpha + \sin 2\alpha.$
followed by rescaling. This boils down to the proof of similar triangles but can be generalized.Dot Product in 3D
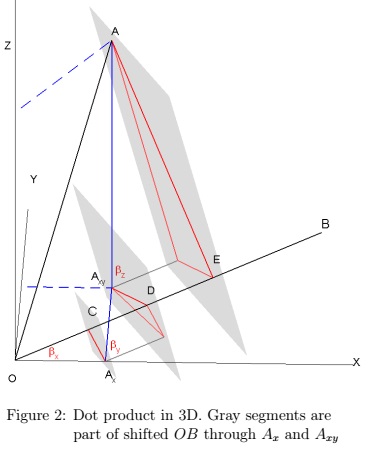
In 3D the coordinates of a unit vector are direction cosines, namely the cosine of the angle the vector makes with each respective axis. (Actually, as $\cos(\pi/2 - \alpha) = \sin\alpha,\;$ the proofs in 2D are visually more appealing using the cosine of the complementary angle, as indicated in Figure 1.)
In Figure 2 the coordinates of $\overrightarrow{A}\;$ are drawn as connected line segments through the points $A_x(a_1, 0, 0),\;$ $A_{xy}(a_1, a_2, 0)\;$ and $A(a_1, a_2, a_3).\;$ We then draw three parallel planes through $A_x,\;$ $A_{xy}\;$ and $A,\;$ perpendicular to $\overrightarrow{B},\;$ giving the point $C,\;$ $D\;$ and $E.\;$ The angles of $\overrightarrow{B}\;$ are $\beta_{x},\;$ $\beta_{y},\;$ $\beta_{z}.$
The projection of $OA_x\;$ on $OB\;$ with angle $\beta_{x}\;$ goes like we did before. For the next segment, one could shift $OB\;$ so that it goes through the point $A_x,\;$ project the segment $A_xA_{xy}\;$ with angle $\beta_{y}\;$ on the shifted $OB\;$ and shift the obtained segment back to $CD.\;$ Finally do the same with the last segment, using the point $A_{xy},\;$ to obtain the segment $DE.\;$ As $AE\;$ is perpendicular to $OB\;$ by construction, one gets the result. Rescaling gives the theorem, proving that we can start with the coordinate formula for positive coordinates. The constructions work for negative coordinates keeping orientation in mind, but the algebraic proofs are then much more elegant.
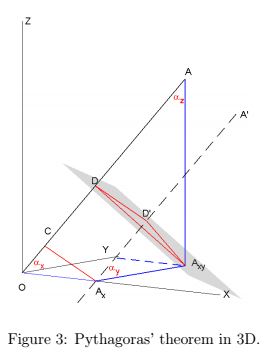
For the Pythagorean theorem, we use a perpendicular plane through $A_x\;$ and $A_{xy}.\;$ Then
$\begin{align} 1 &= |OC| + |CD| + |DE|\\ &= |OA_x|\cos\alpha_{x} + |A_xA_{xy}|\cos\alpha_{y} + |A_{xy}A|\cos\alpha_{z}\\ &=\cos^2\alpha_x+\cos^2\alpha_y + \cos^2\alpha_z. \end{align}$
Rescaling gives the Pythagorean theorem in 3D.
(The figures were drawn with Matlab R2014a)
![]()
73582076
