A Rectangle in Three Circles by Hirotaka Ebisui

First note that if two circles $(CEX)$ and $(DFX)$ are tangent at $X$ the the chords $CE$ and $DF$ are parallel:

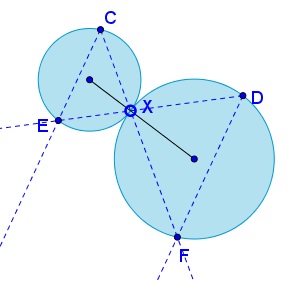
To see that, draw the common tangent at $X$ and recollect the properties of inscribed angles.

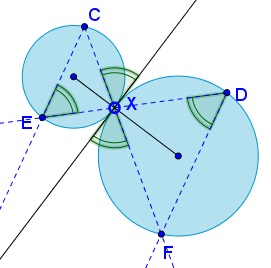
Thus, $ABDC$ is an isosceles trapezoid.

In circle $(CMEX),$ $\angle MCE=\angle MXE=\angle DXN.$ On the other hand, $\angle MCE=\angle MCA$ and in circle $(MCDN),$ $\angle MCA=\angle MNA.$ It follows that $\angle DXN=\angle MNA=\angle XNA,$ which makes $DI\parallel AN.$ Similarly, $BM\parallel CH.$

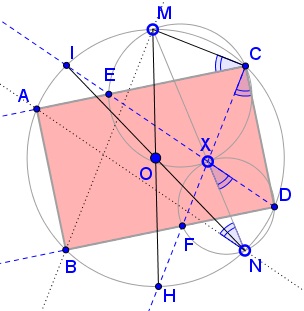
In circle $(CMEX),$ since $MX$ is a diameter, $\angle MCX=90^{\circ}.$ But $\angle MCX=\angle MCH,$ where $H$ is the second intersection of $CX$ with $(MCDN).$ It follows that $MH$ s a diameter in $(MCDN).$ Similarly, $NI$ is a diameter in $(MCDN).$ Thus $\overset{\frown}{MI}=\overset{\frown}{NH}.$ In addition, since $DI\parallel AN,$ $\overset{\frown}{AI}=\overset{\frown}{DN}.$ Thus,

$\overset{\frown}{AM}=\overset{\frown}{AI}+\overset{\frown}{MI}=\overset{\frown}{DN}+\overset{\frown}{NH}=\overset{\frown}{DH}.$

From this we deduce that $\angle MCA=\angle HCD,$ and, as a consequence $\angle ACD=\angle MCH=90^{\circ}.$ So, in the isosceles trapezoid $ABDC$ one of the angles is $90^{\circ},$ which makes it a rectangle.

• Let $S$ be the point of intersection of the lines $MC,$ $ND,$ as the radical center of the circles $(O)$ (the circumcircle of the quadrilateral $MCDN),$ $(K)$ (the circumcircle of $\Delta CMX)$ and $(L)$ (the circumcircle of $\Delta DNX).$

  

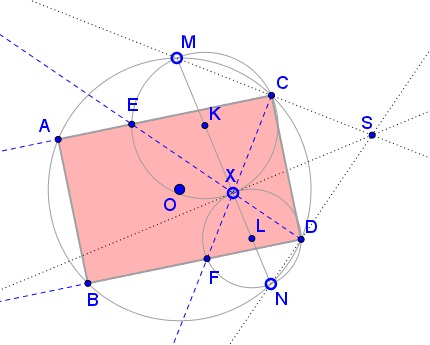
  So, we have that

  (1)

  $SX\perp MN$

  (the line through the point $X$ and perpendicular to the line $MN,$ as the radical axis of the circles $(K),$ $(L),$ passes through the point $S = MC\cap ND,$ where $MC = (O)\cap (K)$ and $ND = (O)\cap (L)).$

• From the cyclic quadrilateral $CSDX$ (because of $\angle XCS = \angle XDS = 90^{\circ})$ we have

  (2)

  $\angle XCD = \angle XSD$

  From the cyclic quadrilateral $XDNF$ we have

  (3)

  $\angle XFD = \angle XND.$

  From (2), (3)

  (4)

  $\angle XCD + \angle XFD = \angle XSD + \angle XND = 90^{\circ}$

• From (4), $\angle CDF = 90^{\circ}$ and, similarly, $\angle ECD = 90^{\circ}.$ Thus we deduce that the quadrilateral $ABCD$ is a rectangle, as required, and the proof is complete.

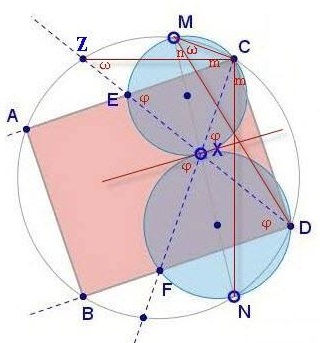
By the Exterior Angle Theorem,

$\begin{align} \angle XEC&=\varphi=\angle EZC+ECZ=\omega+m\\ \angle XMC&=\varphi=\angle DMC+\angle NMD=\omega+n, \end{align}$

implying (together with $\angle XEC=\angle XMC)$ $m=n.$ It follows that

$\displaystyle \begin{align} \angle ZCA=\angle NCD&\Rightarrow\;\angle ZCA+\angle ACN=\angle NCD+\angle ACN\\ &\Rightarrow\;\angle ZCN=\angle ACD. \end{align}$

But $\angle ZCN=\angle ZDN=90^{\circ},$ so that $\angle ACD=90^{\circ}.$ Similarly, $\angle BDC=90^{\circ}.$ Hence $ABDC$ is a rectangle.

Let $\angle XCE=\alpha$ and $\angle MCE=\beta;$ $\alpha+\beta=90^{\circ}.$

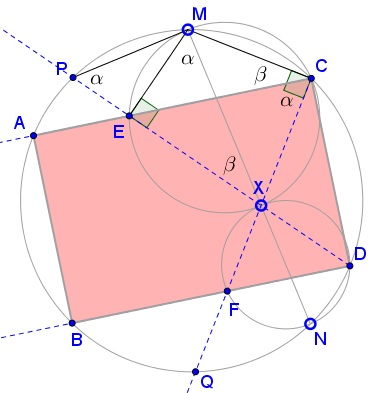
$\left.\begin{align} &\angle PMN=\angle PDN=90^{\circ}\\ &\angle MCQ=\angle MNQ=90^{\circ} \end{align}\right\}\Rightarrow\;PM\parallel QN\Rightarrow PM=QN.$

$\angle XCE=\angle XME=\angle EPM=\alpha.$ In $\Delta PMN,$ $\angle PMN=90^{\circ},$ $\angle MPN+\angle MNP=90^{\circ},$ $\angle MPX=\alpha,$ therefore $\angle XPN+\angle MNP=\beta.$

From $PM=QN,$ $\angle MNP=\angle NMQ,$ so that $\beta=\angle NMQ+\angle DPN=\angle DCQ.$

$\angle DCA=\angle DCQ+\angle QCA=\beta+\alpha=90^{\circ}.$ Similarly, $\angle CDB=90^{\circ}.$ Further, $\angle ACD+\angle DBA=180^{\circ},$ implying $\angle ABD=90^{\circ}$ and making $ABDC$ a rectangle.

Let $\angle NXD=\alpha,$ then $\angle EXM=\alpha$ and $\angle XND=90^{\circ}-\alpha, since $\Delta XND$ is a right triangle.

Since $MNDC$ is a cyclic quadrilateral, $\angle MCD+\angle MND=180^{\circ}.$ So $\angle MCD=90^{\circ}+\alpha.$ But, since $\angle MCE=\angle EXM=\alpha$ (as inscribed angles subtended by the same arc $\overset{\frown}{EM},)$ $\angle ACD$ must be right angle. Since $FD\parallel EC,$ $ABDC$ is a rectangle.

This is a problem by Hirotaka Ebisui described in a paper The New Temple Geometry Problems in Hirotaka's Ebisui Files by Miroslaw Majewski, Jen-Chung Chuan, Nishizawa Hitoshi.

Solution 2 is by Kostas Vittas; Solution 3 is by Thanos Kalogerakis; Solution 4 is by David Nguyen; Solution 5 is by Mike Lawler.

Four of the five solutions are by pure angle chasing.