Novel Concurrency of Perpendicular Bisectors
What is this about?
Problem
Three circles with chords $AB,$ $BC,$ and $CA$ cross the side lines of $\Delta ABC$ in points $A_c,$ $B_c;$ $B_a,$ $C_a;$ $C_b,$ $A_b,$ as in the diagram
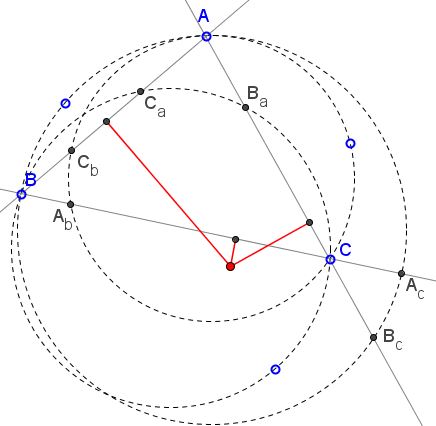
Prove that the perpendicular bisectors of $A_{b}A_{c},$ $B_{a}B_{c},$ $C_{a}C_{b}$ are concurrent.
Proof
The proof depends on the a lemma placed on a separate page. Denote $X=A_{c}B_{c}\cap A_{b}C_{b}.$ According to the lemma, $\Delta A_{b}A_{c}X$ is isosceles so that the perpendicular bisector of $A_{b}A_{c}$ is simultaneously the angle bisector of the angle at $X.$
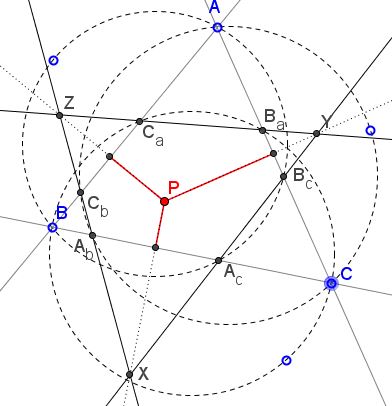
If we similarly introduce the intersections $Y$ and $Z,$ we'll find that the perpendicular bisectors in question double as angle bisectors in $\Delta XYZ$ and, therefore concur in its incenter.
Acknowledgment
The statement and the proof are due to Emmanuel Antonio José García (Dominican Republic).
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73582397
