Garcia's Two Circles Lemma

What is this about?

Problem

In $\Delta ABC,$ a circle with $BC$ as a chord meets $AC$ at $G$ and $AB$ at $E.$ Another circle with $AC$ as a chord meets $BC$ at $K$ and $AB$ at $M.$ $N$ is the intersection of $KM$ and $EG.$

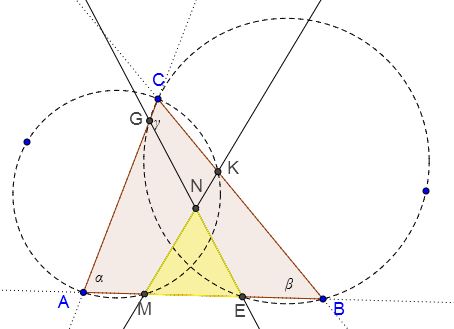
Concurrency of the perpendicular bisectors - lemma

Prove that $EN=MN.$

Proof

The proof employs angle chasing. Let $\angle ACB=\gamma.$ Since quadrilateral $AMKC$ is cyclic, $\angle ACK+\angle AMK=180^{\circ},$ implying $\angle AMN=180^{\circ}-\gamma.$ In other words, $\angle EMN=\gamma.$ Similarly, since quadrilateral $BEGC$ is cyclic, $\angle MEN=\gamma.$

It follows that $\Delta EMN$ is isosceles and $EN=MN,$ as required.

Note: The circles may cross the side lines of the triangle in points either interior or exterior to the sides. The reasoning in cases other than that considered above requires only minor adjustments.

Acknowledgment

The statement and the proof are due to Emmanuel Antonio José García (Dominican Republic).

72103960