Inradii Relation in Right Triangle

Source

Leo Giugiuc has kindly posted at the CutTheKnotMath facebook page a problem due to Borislav Mirchev, originally from Perú Geométrico forum:

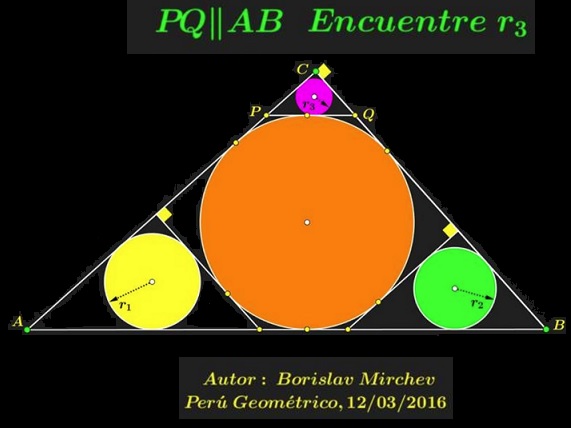
Inradii Relation in Right Triangle - source

It could have been a Sangaku from a couple of centuries ago.

Problem

$\Delta ABC\;$ is right-angled at $C;\;$ $PQ\parallel AB\;$ and tangent to the incircle of $\Delta ABC.\;$ Two more tangents are drawn perpendicular to the legs of the triangle, thus creating three right triangles similar to $\Delta ABC.$

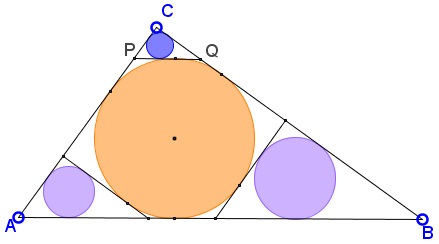
Inradii Relation in Right Triangle - problem

Denote the incircles of these triangles as $(A),\;$ $(B),\;$ $(C)\;$ and their inradii $r_1,\;$ $r_2,\;$ $r_3,\;$ respectively. Find the relationship between the three radii.

Solution 1

Triangles $CPQ\;$ and $CAB\;$ are similar = let $k\;$ be the similarity ratio and set $S=\Delta ABC],\;$ the area of $\Delta ABC.\;$ The incircle of $\Delta ABC\;$ is an excircle of $\Delta CPQ.\;$ It follows that $\displaystyle r=\frac{k^2S}{k(p-c)}=\frac{kS}{p-c}.\;$ On the other hand, $\displaystyle r_3=\frac{k^2S}{kp}=\frac{S}{p},\;$ from which $\displaystyle r_3=\frac{r}{p}(p-c).\;$ Similarly, $\displaystyle r_1=\frac{r}{p}(p-a)\;$ and $\displaystyle r_2=\frac{r}{p}(p-b).\;$ Introduce $x=p-a,\;$ $y=p-b,\;$ and $z=p-c.\;$ Then $a=y+z\;$ $b=z+x,\;$ and $c=x+y.\;$ By the Pythagorean Theorem,

$(y+z)^2+(z+x)^2=(x+y)^2,$

so that $z^2+(x+y)z-xy=0,\;$ or, $\displaystyle z=\frac{\sqrt{(x+y)^2+4xy}-(x+y)}{2}.\;$ From here

$\displaystyle r_3=\frac{\sqrt{(r_1+r_2)^2+4r_1r_2}-(r_1+r_2)}{2}.$

Solution 2

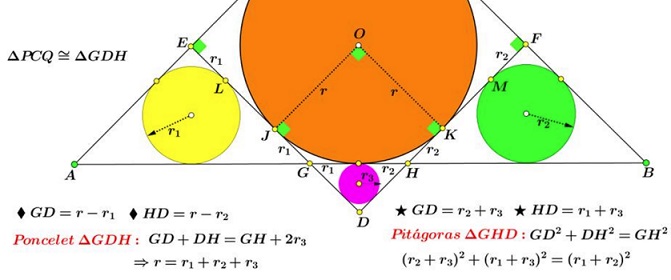
Inradii Relation in Right Triangle - solution 2

Acknowledgment

Solution 1 is by Leo Giugiuc and Dan Sitaru; Solution 2 is by Miguel Ochoa Sanchez.

71921540