Fixed Point on Perpendicular Bisector

What Might This Be About?

Problem

Let two circles $(C_{1}),$ $(C_{2})$ intersect at two points $A$ and $B$ and a variable line through $A$ cut circle $(C_{1})$ in $P_1$ and circle $(C_{2})$ in $P_2.$

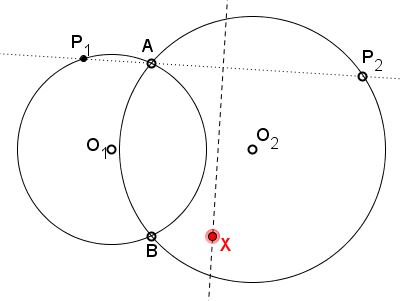
fixed point on the perpendicular bisector - problem

Prove that the perpendicular bisector of line $P_{1}P_{2}$ passes through a fixed point.

Solution

We know that $\angle P_{1}BP_{2}$ does not depend on the position of $P_{1},P_{2},$ making all triangles $P_{1}BP_{2}$ similar, and implying that the same is true for triangles $P_{1}MB,$ where $M$ is the midpoint of $P_{1}P_{2}.$ As a consequence, $\angle AMB$ remains constant.

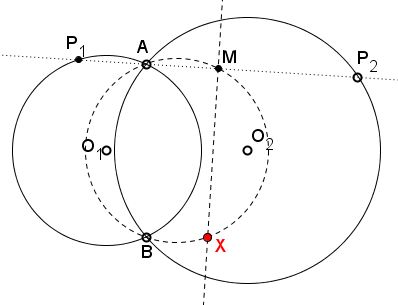
fixed point on the perpendicular bisector - solution

This means that when the line $P_{1}P_{2}$ moves point $M$ describes a circle, say circle $(O).$

Let $X$ be the intersection of the perpendicular bisector of $P_{1}P_{2}$ and the perpendicular to $AB$ at $B.$ Since both angles $AMX$ and $ABX$ are right, the quadrilateral $AMXB$ is cyclic and is thus circumscribed by $(O).$ It follows that $X$ is the intersection of the perpendicular bisector with $(O)$ such that $AX$ is the diameter of $(O).$ Since the latter does not depend on the position of $P_{1}P_{2},$ the same is true of $X.$

Acknowledgment

The problem has been posted by Walid Malek (Marocco) at the Short Mathematical Idea facebook page.

71528396