The Eutrigon Theorem

What is this about?

Problem

W. Roberts (2003) introduced the term Eutrigon for a triangle (in general scalene), with one angle equal \(60^{\circ}\). The side opposite the \(60^{\circ}\) angle is called (unfortunately in my view) the hypotenuse, the other two sides are called the legs.

The area of any eutrigon is equal to the sum of the areas of the equilateral triangles on its legs, minus the area of the equilateral triangle on its hypotenuse.

Eutrigon and Eutrigon's theorem - problem

Hint

Try to embed an eutrigon into a bigger equilateral triangle in a manner that leaves off two equilateral triangles and a parallelogram.

Solution

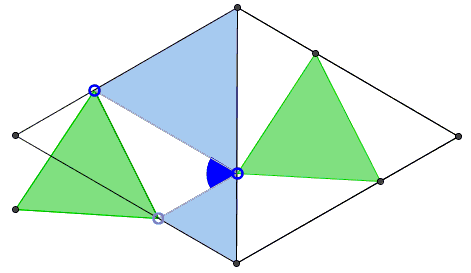
Eutrigon and Eutrigon's theorem - proof

Let the legs of an eutrigon be \(a\) and \(b\) and the hypotenuse \(c\), \(A\) its area and \(A(x)\) the area of an equilateral triangle with side \(x\), then what we see in the applet can be expressed by two equations:

\(A(a+b)=A(a)+A(b)+2A\) and
\(A(a+b)=A(c)+3A\),

from which the theorem follows.

Acknowledgment

This is a JavaScript/HTML5 version of an older applet prepared with GeoGebra.

71940076