Equilateral Triangle on a Closed Curve
What is this about?
Problem
On any simple closed curve there exist three points that are vertices of an equilateral triangle.
Acknowledgment
I came across this problem and its solution in M. Chamberland's Single Digits. In Praise of Small Numbers (Princeton University Press, 2015), pp. 123-124. The section it is in begins with the Inscribed Square Problem which was posed by Otto Toeplitz in 1911, and, for this reason, is often refers to as the Toeplitz Problem. It's the same as above, except that we are now seeking four points that are vertices of a square. The existence of a square has been established for sufficiently smooth curves, but not in general case.
The problem with a triangle comes as a consolation prize - this one admits a relatively simple solution that l present below.
Proof
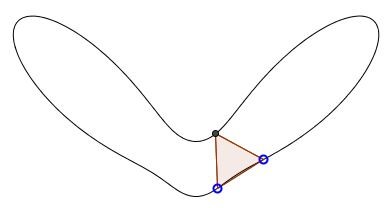
Recollect that a (planar) curve is a continuous mapping $f$ of the interval $[0,1]$ into the plane $\mathbb{R}^2.$ The curve is closed if $f(0)=f(1)$ and is simple if, for no other pair $a,b\in [0,1],$ $f(a)=f(b),$ i.e., if the curve has no self-intersections. According to the Jordan Curve Theorem, the curve separates the plane into two regions - its interior and exterior. Start with a small equilateral triangle with two vertices on the curve and the third one in the curve's interior:
By shifting the points along the curve while keeping the third one as the vertex of an equilateral triangle (with a fixed orientation) we make an assumption of continuity, viz., that the third vertex moves continuously with the two base points.
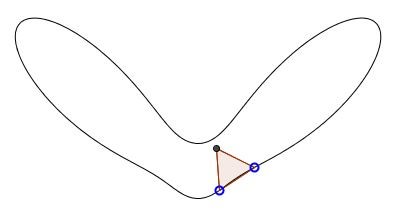
At the beginning the third vertex was found in the interior of the curve and it will stay in the interior for some positions of the base points. Now, move the two as far as possible. When the base of the triangle is the longest chord of the curve, the third vertex could no longer be in its interior. It is either on the curve - and we should look no further, or it's in the exterior of the curve:

By the continuity of its dependency on the position of the base points, there bound to be a position of the two for which the third point crossed the curve. That settles the problem.
![]()
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73574140
