Equilateral Triangle from Equilateral Triangle
What Is This About?
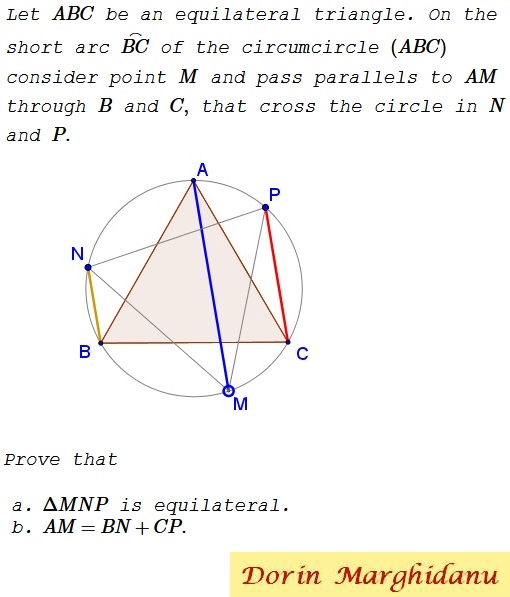
Problem
Solution 1
For the first part, we shall prove a little more general result:
Let $ABC$ be an acute triangle. On the short arc $\overset{\frown}{BC}$ of the circumcircle $(ABC)$ consider point $M$ and pass parallels to $AM$ through $B$ and $C,$ that cross the circle in $N$ and $P.$ Then $\Delta MNP$ is equal to $\Delta ABC.$
Observe, that since $BN\parallel AM,$ $\overset{\frown}{AN}=\overset{\frown}{BM}$ and, similarly, $\overset{\frown}{AP}=\overset{\frown}{CM}.$ It follows that
$\begin{align} \angle MPN&=\angle BPM+\angle BPN=\angle ACN+\angle BCN\\ &=\angle ACB. \end{align}$
Similarly, $\angle MPN=\angle ABC,$ which proves that the two triangle are similar. Since they have the same circumcircle, they are actually equal.
Concerning the second part, note that, since $\angle NMP=60^{\circ},$ $\overset{\frown}{NAP}=120^{\circ}.$ And, since $\angle ABC=60^{\circ},$ $\overset{\frown}{APC}=120^{\circ}.$ It follows that $AN=PC.$ By symmetry, $AN=PC=BM.$ Similarly, $CM=AP=BN.$
The lines through $C$ and $P,$ parallel to $BM,$ pass through $N$ and $P.$
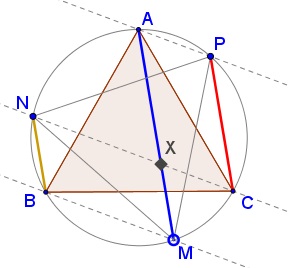
Let $X$ be the intersection of $AM$ with $CN.$ Then $APCX$ and $MBNX$ are parallelograms: $AX=CP,$ $MX=BN,$ proving the second part.
Solution 2
Recollect that if $\Delta XYZ$ is inscribed in the unit circle then it's equilateral iff $X+Y+Z=0.$ Indeed, $\Delta XYZ$ is equilateral iff its centroid $\displaystyle G=\frac{X+Y+Z}{3}$ coincides with the origin, meaning exactly that $X+Y+Z=0.$
Choose $A=1,$ $B=u,$ $\displaystyle C=\frac{1}{u},$ $\displaystyle u=-\frac{1}{2}+i\frac{\sqrt{3}}{2}.$ Let $M=m,$ $N=n,$ $P=p.$ From $BN\parallel AM,$ $\displaystyle \frac{N-B}{M-A}=\overline{\left(\frac{N-B}{M-A}\right)},$ implying $\displaystyle \frac{n-u}{m-1}=\frac{\displaystyle \frac{1}{n}-\frac{1}{u}}{\displaystyle \frac{1}{m}-1},$ i.e., $\displaystyle n=\frac{m}{n}.$ Similarly, $p=mu.$ It follows that $\displaystyle M+N+P=m(1+u+\frac{1}{u}=0,$ so that $\Delta MNP$ is equilateral.
Also,
$\displaystyle BN=\left|\frac{m}{u}-u\right|=|mu-1|=\left|m-\frac{1}{u}\right|=CM.$
Similarly, $CP=BM.$ $But, from van Schooten's theorem, $BM+CM=AM.$
Acknowledgment
The problem has been kindly posted by Dorin Marghidanu at the CutTheKnotMath facebook page. Solution 2 is by Leo Giugiuc.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581714
