Orthogonality in Isogonal Conjugacy
What Might This Be About?
Problem
$BD$ and $BE$ are isogonal conjugate in $\Delta ABC;\;$ $BE\perp CE\;$ and $BD\perp A.\;$ $F$ is the intersection of $CD\;$ and $AE.$
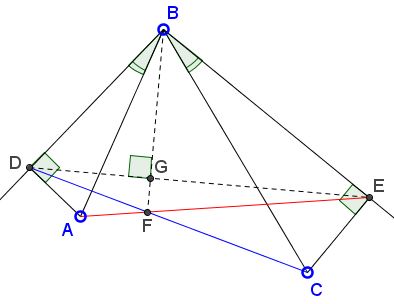
Prove that $BF\perp DE.$
Solution
Obviously, the angles $BDC$ and $BEA$ are acute. Consequentely, the angles $BDE$ and $BED$ are also acute. So, without loss of generality, we may choose $D = -u,$ $E = v$ and $B = i,$ whith $u, v \gt 0.\;$ On the other hand, triangles $BDA$ and $BEC$ are inversely similar and right angled at $D$ and $E,$ respectively; hence there is $k \gt 0\;$ such that $\displaystyle\frac{A-D}{B-D}=\overline{\left(\frac{C-E}{B-E}\right)}=-ki.\;$ From here, $A=k-u-uki\;$ and $B=v-k-vki.\;$ Let's write the equations of the straight lines $AE\;$ and $CD:\;$
$\begin{cases} AE:& ukx - (u + v - k)y = uvk,\\ CD:& vkx + (u + v - k)y = -uvk. \end{cases}$
These give us $x=0,$ meaning that $F$ lies on the $y\text{-axis}.$ But $DE$ was chosen to be the $x\text{-axis}\;$ and the two meet at the right angle.
Acknowledgment
The problem that is due to Elberling Vargas Diaz (Peru) has been communicated to me by Leo Giugiuc along with a solution by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc (Romania).
Remark
Francisco Javier García Capitán has observed that, for a given line $BE,\;$ there is a second line, and likelely to be more, that posses the property of line $BD.\;$ He posed this as an algebraic problem:
If we consider the vertices with coordinates $B=(0,0),$ $C=(a,0),$ and $A=(u,v),$ the lines $y=mx\;$ and $y=nx\;$ are isogonal with respect to the angle $B\;$ if $\displaystyle n=\frac{v-mu}{u+mv}.\;$ For any $m\;$ there exists another value of $n,\;$ precisely $\displaystyle n=\frac{a+am^2-u-mv}{m(u+mv)}\;$ such that the lines $y=mx\;$ and $y=nx\;$ satisfy the conditions of the problem. Give some geometric description of this line.
The statement we are looking for is this:
Given $\Delta ABC$ line $BV.$ Find line $BW$ and points $D\in BV\;$ and $E\in BW\;$ such that (1) $AD\perp BD,\;$ (2) $CE\perp BE,\;$ and (3) $BF\perp DE$ where $F=CD\cap AE.$
The statement above by Elberling Vargas Diaz asserts that the isogonal conjugate to line $BV\;$ solves that problem. There are indeed more extra lines that may be said to represent degenerate cases.
Let $(BC)$ denote the circle with $BC\;$ as a diameter. Define $D\in BV\;$ such that $AD\perp BV;\;$ $E=CD\cap (BC).\;$ Then (1) $AD\perp BD,\;$ (2) $CE\perp BE,\;$ and since $E\in BC,\;$ $F=AE\cap CD=E,\;$ $(3) BF\perp CD.$ Thus $BE$ is the sought line.
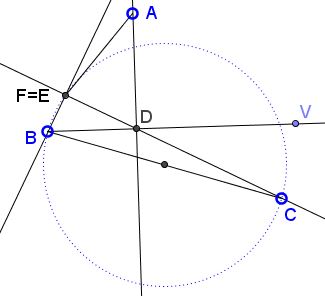
Francisco Javier García Capitán found two more. Let $D$ be constructed as above: $AD\perp BV.\;$ Then line $AD\;$ intersects $(BC))\;$ in, say, $X\;$ and $Y.\;$

Taking $F=D$ and either $E=X\;$ or $E=Y\;$ shows that the lines $BX\;$ and $BY\;$ also solve the problem.
Note that we could have started with the circle $(AB),\;$ with a diameter $AB\;$ which would have led to three additional lines.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579608
