Droz-Farny Theorem - an Analytic Solution
What Might This Be About?
Problem
Let two perpendicular lines pass through the orthocenter $H\;$ of $\Delta ABC.\;$ Assume they meet the sides $AB,$ $AC,$ and $BC$ in $C_1,\;$ $B_1,\;$ $A_1\;$ and $C_2,\;$ $B_2,\;$ $A_2,\;$ respectively. Let $t\in [0,1].\;$ Define $M_1= tA_1+(1-t)A_2,\;$ $M_2=tB_1+(1-t)B_2,\;$ and $M_3=tC_1+(1-t)C_2.$
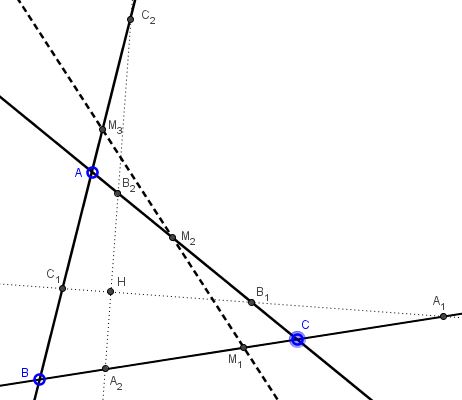
Prove that $M_{1},\;$ $M_{2}\;$ and $M_3\;$ are collinear.
Solution
As has already been done previously, we choose to place the origin of the coordinate system at the orthocenter and the axes along the two given lines. We thus may specify the coordinates of the points involved: $A_{1}(a,0),$ $A_{2}(0,b),\;$ $B_{1}(c,0),$ $B_{2}(0,d),\;$ $C_{1}(e,0),$ $C_{2}(0,f).\;$ From here, $M_{1}(ta,(1-t)b),\;$ $M_{2}(tb,(1-t)d),\;$ $M(te,(1-t)f).$
The three points are collinear iff
$\left|\begin{array}{ccc} ta & (1-t)b & 1 \\ tc & (1-t)d & 1 \\ te & (1-t)f & 1 \end{array}\right|= t(1-t)\left|\begin{array}{ccc} a & b & 1 \\ c & d & 1 \\ e & f & 1 \end{array}\right|=0, $
We may exclude cases where $t=0$ or $t=1$ as trivial because then the three midpoints all lie on one of the given lines and are, therefore, automatically collinear:

Thus the collinearity of the three points is equivalent to the determinant identity:
(0)
$\left|\begin{array}{ccc} a & b & 1 \\ c & d & 1 \\ e & f & 1 \end{array}\right|=0, $
Note that segment $A_1A_2$ lies on the side line $BC$ of $\Delta ABC,\;$ and, therefore, the latter has the slope $-b/a.$ Let $A=(x_{1},y_{1}).\;$ Then since $AH\perp BC,$
(1)
$ax_{1}-by_{1}=0.$
Similarly, with $B=(x_{2},y_{2})\;$ and $C=(x_{3},y_{3}),$
(2)
$cx_{2}-dy_{2}=0$ and
(3)
$ex_{3}-fy_{3}=0.$
Now, again, since $A_1A_2$ and $BC$ define the same line, its equation is
(4)
$bx+ay=ab.$
In particular, $bx_{2}+ay_{2}=ab$ and $bx_{3}+ay_{3}=ab.\;$ Thus we can solve (2) and (4) for $x_2$ and $y_2,\;$ whereas from (3) and (4) we can obtain for $x_3\;$ and $y_3.\;$ Let's focus on $x_2\;$ and $y_2:$
(5)
$\displaystyle x_{2}=\frac{abd}{ac+bd}, \space y_{2}=\frac{abc}{ac+bd}.$
But we can also use the fact that $B\;$ lies on $AB,\;$ i.e., $C_1C_2.\;$ Since the equation of the latter is $fx+ey=ef,\;$ we have $fx_{2}+ey_{2}=dc.\;$ Solving this together with (2) gives,
(6)
$\displaystyle x_{2}=\frac{def}{ce+df}, \space y_{2}=\frac{cef}{ce+df}.$
Equating the two expressions for either $x_2\;$ or $y_2\;$ we obtain
(7)
$ab(ce+df)=ef(ac+bd).$
The latter expression is equivalent to
(7' )
$ace(b-f)=bdf(e-a).$
Proceeding similarly for $A\;$ and $C\;$ yields additional identities $ef(ac+bd)=cd(ae+bf)\;$ and $cd(ae+bf)=ab(ce+df).\;$ Between them, the three identities hold three equal quantities. We'll need just (7'). Let's return to the determinant in (0):
(8)
$\left|\begin{array}{ccc} a & b & 1 \\ c & d & 1 \\ e & f & 1 \end{array}\right|= \left|\begin{array}{ccc} a & b & 1 \\ c & d & 1 \\ e-a & f-b & 0 \end{array}\right|. $
We may assume that none of the six quantities $a,b,c,d,e,f\;$ is $0,\;$ for, otherwise, one of the vertices lies on one of the given lines, making it an altitude. For example, if $b=0\;$ the second line is the altitude through $A,\;$ whereas the first is parallel to $BC:$
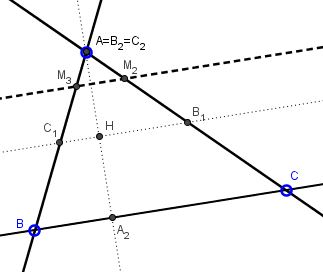
In this case, $M_2M_3\parallel BC,\;$ $M_1\;$ is the point at infinity of the pencil of lines parallel to $BC,$ making the three points collinear. We thus assume that $abcdef\ne 0$ and proceed to modify the determinant in (8). With (7') in mind:
$ abcdef\left|\begin{array}{ccc} a & b & 1 \\ c & d & 1 \\ e-a & f-b & 0 \end{array}\right| = \left|\begin{array}{ccc} abdf & abce & 1 \\ bcdf & acded & 1 \\ bdf(e-a) & ace(f-b) & 0 \end{array}\right|$
We continue with the determinant on the right. Invoking (7') and (7):
$\begin{align} \left|\begin{array}{ccc} abdf & abce & 1 \\ bcdf & acded & 1 \\ bdf(e-a) & ace(f-b) & 0 \end{array}\right| &= \left|\begin{array}{ccc} abdf & abce+abdf & 1 \\ bcdf & acde+bcdf & 1 \\ bdf(e-a) & 0 & 0 \end{array}\right|\\ &=bdf(e-a)[abce+abdf-acde-bcdf]\\ &=bdf(e-a)[ab(ce+df)-cd(ae+bf)]\\ &=0. \end{align}$
Which shows the required collinearity.
Acknowledgment
The proof is a slight modification of the one supplied by Leonard Giugiuc (Romania). A synthetic proof for the case of $t=1/2$ could be found on a separate page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579442
