Vietnamese Lemma towards an Extension of a Japanese Theorem
What Might This Be About?
Problem
Let $O$ be the circumcenter, $I$ the incenter, of $\Delta ABC.$ Let $A'$ be the middle of the arc $BC$ opposite $A;$ and define similarly $C',$ relative to $C.$ Also, let $A'',$ $C''$ b on $OA$ and $OC,$ respectively, such that $OA''=OC''.$ Finally, let $T$ be the second intersection of $A''BC)$ and $(ABC'').$
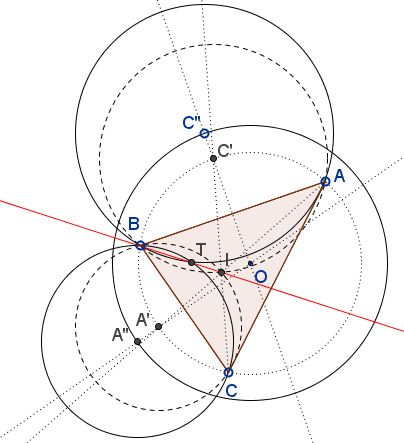
Then $B,$ $T,$ and $I$ are collinear. In Other words, T lies on the bisector of $\angle ABC.$
Proof
It was shown elsewhere that the centers of the circles $(ABI)$ and $(BCI)$ lie on the circumcircle $(ABC) at the midpoints of the corresponding arcs.$
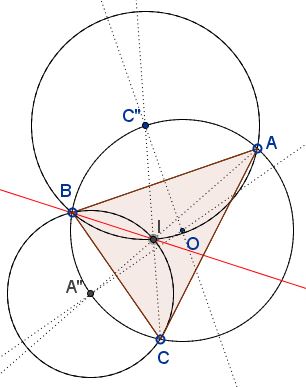
The inverse is proved by reductio ad absurdum. Thus we have that when $A''=A'$ and $C''=C',$ $T = I.$
When the distance between $O$ and $A'', C''$ changes, the line $A''C''$ remains perpendicular to $BI,$ such that the intersection with $BI$ serves as the midpoint between $B$ and $T.$ But that intersection lies on $BI$ and, therefore, so does $T.$
Acknowledgment
The lemma is one part of a result by Dao Thanh Oai (Vietnam) posted at the CutTheKNotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73592504
