Dao's Archimedean Twins - Third Pair
Problem
Consider an arbelos formed by semicircles $(O_{1}),$ $(O_{2}),$ and $(O)$ of radii $a,$ $b,$ and $a + b.$ The famous Archimedean twin circles in an arbelos have equal radii $\displaystyle\frac{ab}{a+b}.$
Let $A_{1}A_{2}$ and $B_{1}B_{2}$ be tangents to the smaller semicircles with $A_{1},$ $B_{1}$ on the line $AB$ and $A_{1}A_{2} = a,$ $B_{1}B_{2} = b.$ Let $H$ and $K$ be the midpoints of the semicircles $(O_{1})$ and $(O_{2})$ respectively, and set $A'' = CH \cap A_{1}B_{2},$ $B'' = CK \cap B_{1}A_{2}.$
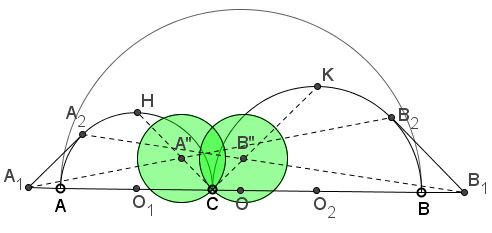
Then the circles through $C$ with centers $A''$ and $B''$ are congruent to the Archimedean twin circles.
Proof
Note that the tangents $A_{1}A_{2}$ and $B_{1}B_{2}$ are easily constructed as $A_{1}A_{2}C$ and $B_{1}B_{2}C$ are simply required to be right isosceles triangles.

Clearly, $\angle ACA_{1} = \angle HCO_{1} = 45^{\circ}.$ Since also $\angle B_{2}B_{1}O_{2} = 45^{\circ},$ lines $CA''$ and $B_{1}B_{2}$ are parallel. Also, $B_{1}O_{2} = \sqrt{2}b.$ Similarly, $A_{1}O_{1} = \sqrt{2}a,$ and $A_{1}B_{1} = (\sqrt{2} + 1)(a + b).$ Therefore, according to Thales' Theorem,
$\displaystyle CA'' = B_{1}B_{2}\cdot\frac{A_{1}C}{A_{1}B_{1}}== b\cdot\frac{(\sqrt{2}+1)a}{\sqrt{2}+1)(a+b)}=\frac{ab}{a+b}.$
Similarly, $\displaystyle CB'' = \frac{ab}{a+b}.$ Therefore, the circles through $C$ with centers $A''$ and $B''$ are indeed Archimedean.
Acknowledgment
The discovery of this pair of Archimedean twins and the proof are due to Dao Thanh Oai. The proof has been published in Forum Geometricorum.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73582683
