Concyclicity from Collinearity

What is this about?

Problem

$B,$ $D,$ $C$ are collinear. $A$ is another point in the plane. Draw $AB,$ $AD,$ $AC,$ as in the figure below. Rotate $AB,$ $AD,$ $AC$ around $B,$ $D,$ $C,$ respectively, by the same angle: $\angle EBA = \angle EDA = \angle FCA.$ $BE$ meets $CF$ in $F;$ $DE$ meets $CF$ in $G;$ $BE$ meets $DE$ in $E.$

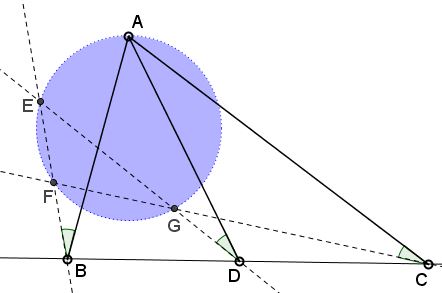
Concyclicity from collinearity - problem

Prove that $AEFG$ is cyclic.

Proof

The proof is pure angle chasing.

From $\angle EBA = \angle EDA$ points $E,$ $B,$ $D,$ $A$ are concyclic. It follows that either $\angle ABD = \angle AED$ or $\angle ABD + \angle AED=180^{\circ}.$

From $\angle ACF = \angle ABF$ points $A,$ $B,$ $C,$ $F$ are concyclic. It follows that $\angle AFC = \angle ABC$ or $\angle AFC + \angle ABC=180^{\circ}.$

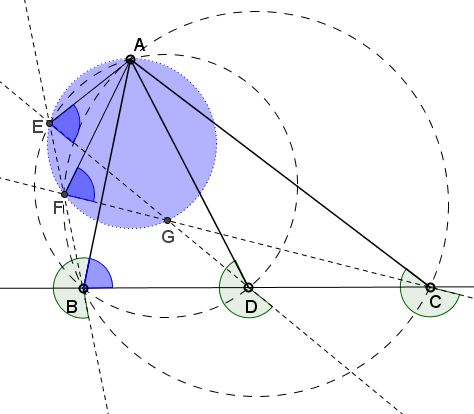
Concyclicity from collinearity - solution

But $ABC$ and $ABD$ are the same angle so that either $\angle AED = \angle AFC$ or $\angle AED + \angle AFC=180^{\circ},$ implying that either $\angle AEG = \angle AFG$ or $\angle AEG + \angle AFG=180^{\circ}$ and, thus, that the four points $A,$ $E,$ $F,$ $G$ are concyclic.

Note: The converse statement is also true:

If points $A,$ $E,$ $F,$ $G$ are concyclic, then points $B,$ $D,$ $C$ are collinear.

Acknowledgment

The statement has been posted at the CutTheNotMath facebook page by Emmanuel Antonio José García (Dominican Republic) in the name of Dao Thanh Oai (Vietnam). The proof is due to Mr. García.

71534825