The Circle of the Orthocenters
What Is That About?
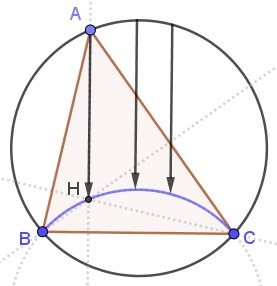
Problem

Solution
Elsewhere it was shown that that the reflection of the orthocenter falls on the circumcircle. Thus if the latter is fixed as well as the line of symmetry, the orthocenter will describe a circle which the reflection of the circumcircle in the side in question.
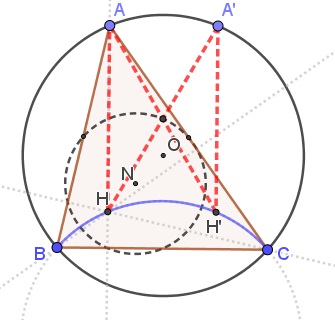
The two circles above are displacements of each other along the line of their centers which explains $AH=A'H'.$
It is well known that the nine-point center $N$ is the midway between the circumcenter $O$ and the orthocenter $H$ and that the circumradius is twice the radius of the nine-point circle. It follows that the circumcircle $(O)$ is homothetic to the nine-point circle $(N)$ in the orthocenter $H$ with the coeffluent of $2.$ In particular, for any point $A'$ on $(O)$ the midpoint of $HA'$ lies on the nine-point circle $(N).$
From 2. it follows that $AH=A'H'$ and, of course, $AH\parallel A'H'.$ implying that $AHH'A'$ is a parallelogram, so that the midpoints of $AH'$ and $A'H$ coincide. Thus the midpoint of $AH'$ lies on $(N).$
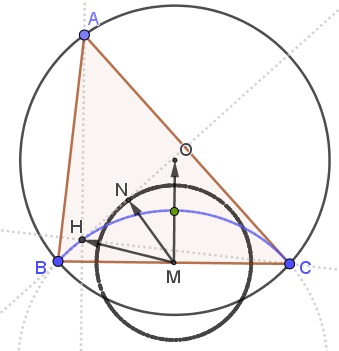
As $A$ varies over $(O),$ $H$ varies over $(O'),$ the reflection of $(O)$ in $BC.$ $\displaystyle N=\frac{O+H}{2},$ so that since $O$ is fixed, $N$ moves over a circle of the radius twice as small as that of $(O'),$ i.e., the radius of $(O).$ This is the radius of the nine-point circle. Due to the symmetry, the circle at hand is its own reflection in $BC$ and is symmetric in it midpoint, proving part 4.
Acknowledgment
The problem was kindly communicated to me by Thanos Kalogerakis who eventually found a simple step-by-step solution. I split the problem into these steps and added a couple of questions of my own.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573141
