Parallelogram with Side Lines through Fixed Points

What Might This Be About?

Statement

If the four side lines of a parallelogram pass through four collinear fixed points, the diagonals, too, pass through fixed points on the same line:

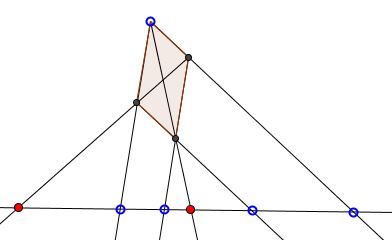
Catalan's theorem - problem

Proof

Denote the point involved as below:

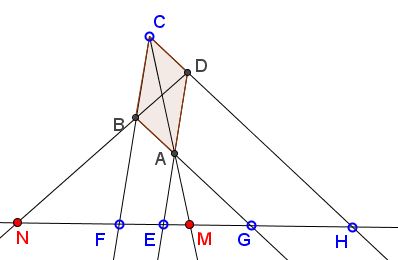
Catalan's theorem - solution

By Thales' theorem,

$\displaystyle\frac{FE}{EM}=\frac{CA}{AM}=\frac{HG}{GM},$

or, $\displaystyle\frac{GM}{EM}=\frac{HG}{FE},$

which means that $M$ divides $EG$ in the ratio $HG:FE.$ Since points $E,F,F,H$ are fixed so is that ratio and, therefore, point $M.$ Point $N$ is fixed for the same reason.

Acknowledgment

In Exercices de Géométrie (Jacques Gabay, 1991, #1124, Theorem 322) F. G.-M. credits E. Catalan with this statement.

72109894