Isosceles Configuration in Triangle
What is this about?
Acknowledgment
The applet above illustrates a problem posted at the CutTheKnotMath facebook page by Bùi Quang Tuän. A similar problem has been posted by Oai Thanh Dao at the Art of Problem Solving forum.
Problem
At vertices of a triangle construct three similar isosceles triangles with bases on opposite sides.
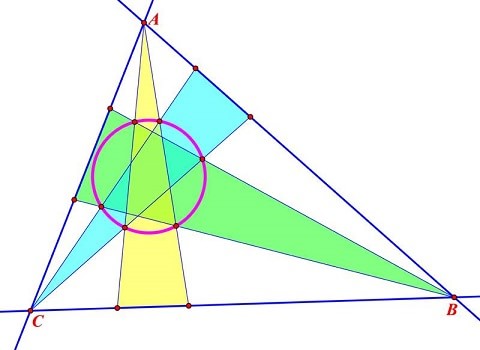
The six sides of these three similar isosceles triangles intersect each other at six concyclic points, as intimated in the above figure.
Proof
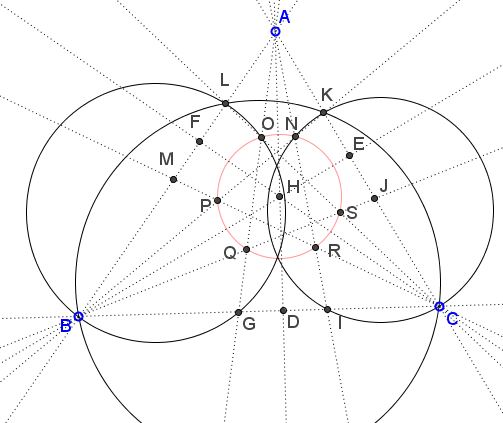
Let's label the diagram as shown below:
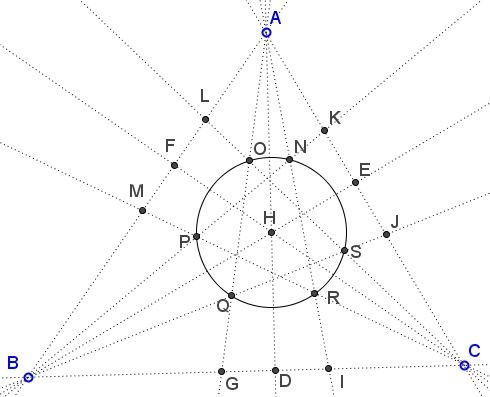
$AD, BE, CF$ are the altitudes of $\Delta ABC; $H$ the orthocenter; $ $AGI, BJK, CLM$ the isosceles triangles; $N,O,P,Q,R,S$ the six points of intersection that ought to be proved collinear. Denote the common apex angle of the three triangles as $2\delta.$ Then, e.g., $\angle NAQ = 2\delta = \angle NBQ,$ implying that points $A,Q,N,B$ are concyclic.
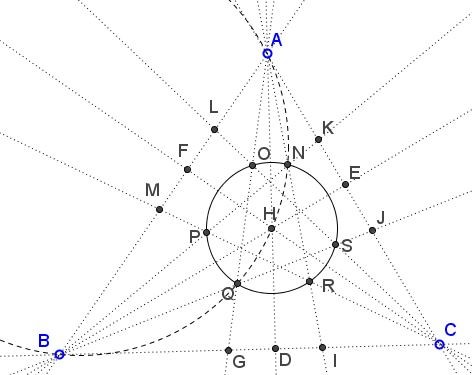
From the diagram at looks like the orthocenter $H$ lies on that circle $(ABQN).$ This is indeed so because both altitudes $AD$ and $BE$ - being the angle bisectors in isosceles triangles - pass through the midpoint of the arc $NQ$ and also meet in $H.$ It follows that not only $H$ is on $(ABQN)$ but is the midpoint of the arc $NQ.$ This immediately implies that $HN=HQ.$ We may similarly conclude that $HO=HR$ and $HP=HS.$ All points out to the fact that $H$ might be the center of a circle through the six points.
To prove that observe $(ABQN)=(AHB),$ the circumcenter of $\Delta ABH.$ Since the reflection of $H$ in $AB$ lies on $(ABC),$ the circumcircle of $\Delta ABC,$ the circumcircles $(ABC)$ and $(ABH)$ are congruent and, therefore, have equal radii. By analogy, circles $(BCH)$ and $(ACH),$ too, have the same radius. Thus, the respective chords $HN, HQ, HO, HR,HP,HS$ subtend equal angles $\delta$ in the three circles of equal radii, so that all six segments are equal and their endpoints concyclic.
Extra observations
Bùi Quang Tuän's configuration is rich in features. Many could be observed with dynamic geometry software like GeoGebra. For example,
- $\Delta NPR=\Delta OQS$ and both are similar to $\Delta ABC.$ (This is easily shown with straightforward angle chasing.)
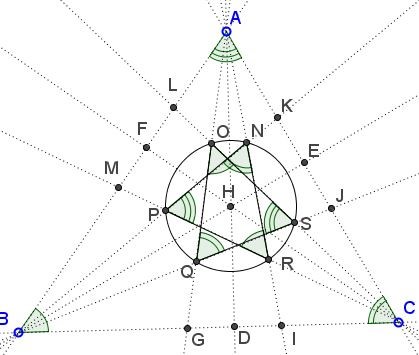
Quintuplets $\{A,L,O,N,K\},$ $\{B,G,Q,P,M\},$ $\{C,J,S,R,I\}$ are concyclic.
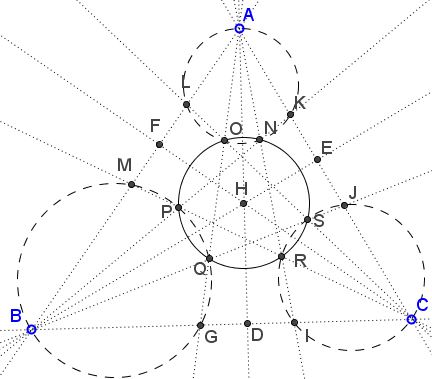
Quintuplets $\{A,J,R,Q,M\},$ $\{B,L,N,S,I\},$ $\{C,K,O,P,G\}$ are concyclic.
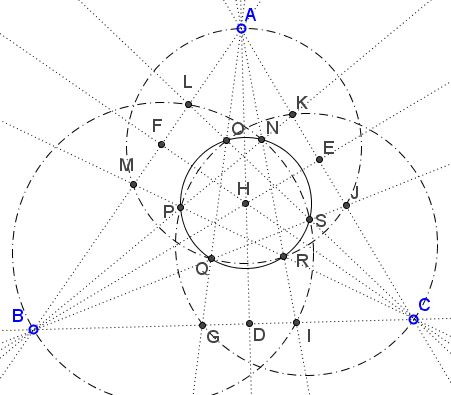
There are parallel lines: $NS\parallel PQ\parallel AC,$ $NO\parallel QR\parallel BC,$ $OP\parallel RS\parallel AB.$
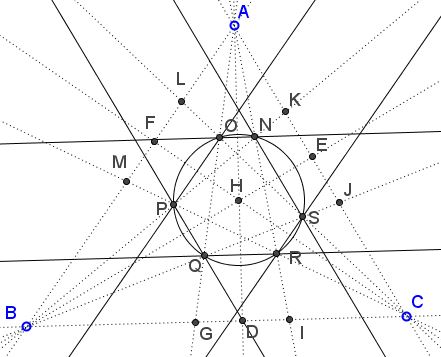
This points to the presence of isosceles trapezoids and, hence, quadruplets of concyclic points.
Second proof
Bùi Quang Tuän has supplied a second proof that also settles the question of there being sets of parallel lines.
By straightforward angle chasing we find that $\angle AMC = \angle AIB,$ implying that $M, B, I, R$ are concyclic; $\angle AJB = \angle AGC,$ implying that $J, C, G, Q$ are concyclic; $\angle BMC = \angle CJB,$ so that $M, B, C, J$ are also concyclic.
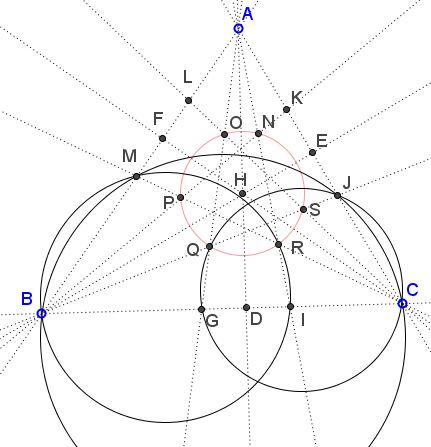
It follows that,
$\begin{align} AQ\cdot AG &= AJ\cdot AC\\ &= AM\cdot AB\\ &= AR\cdot AI, \end{align}$
and, since $AG=AI,$ $AQ=AR,$ making $\Delta AQR$ isosceles and implying that $QR\parallel BC$ and $HQ=HR.$ Similarly, $HN=HS$ and $HO=HP.$
Following in the same vein, we find another triple of quadruplets of concyclic points:
from which
$\begin{align} AO\cdot AG &= AL\cdot AB\\ &= AK\cdot AC\\ &= AN\cdot AI, \end{align}$
which shows that $AO=AN,$ as before, $HN=HO$ and $NO\parallel BC.$ Similarly, $HP=HQ$ and $HR=HS,$ implying that all six points $N,O,P,Q,R,S$ are equidistant from $H.$
![]()
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73578735
