A Problem from the 1985 Balkan Mathematical Olympiad (Shortlist)
Problem
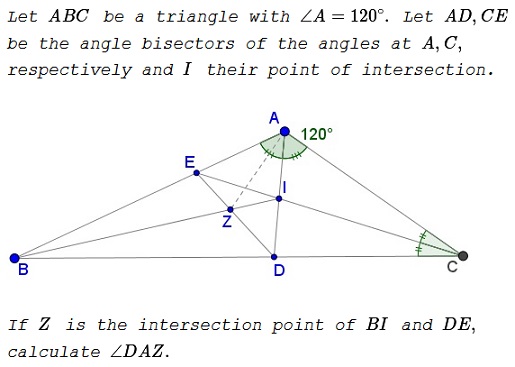
Solution 1
Let $AB=c,\,$ $AC=b,\,$ $BC=a.\,$ We know that $\displaystyle AD=\frac{\displaystyle 2bc\cos\frac{A}{2}}{b+c}\,$ and, since $\angle A=120^{\circ},\,$ $\displaystyle AD=\frac{bc}{b+c}.$
On the other hand, by the property of angle bisectors, $\displaystyle BD=\frac{ac}{b+c},\,$ implying $\displaystyle \frac{BD}{AD}=\frac{a}{b}=\frac{BE}{AE}.$
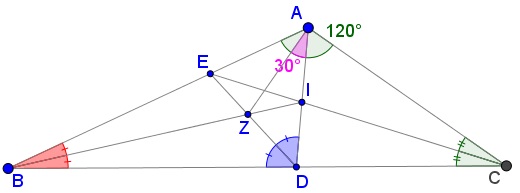
It follows, by the inverse of the angle bisector theorem in $\Delta ABD,\,$ that $DE\,$ is the bisector at angle $D,\,$ so that $Z\,$ is the incenter of $\Delta ABD\,$ and $AZ\,$ the third angle bisector, making $\angle DAZ=30^{\circ}.$
Solution 2
Draw $DF\parallel AB.\,$ By the Exterior Angle Theorem, $\angle AFD=\angle FDC+\angle FCD=\angle ABC+\angle FCD=60^{\circ},\,$ making $\Delta ADF\,$ equilateral. In particular, $AF=AD.$
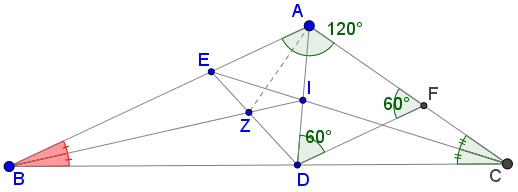
By the Internal Angle Bisector theorem, $\displaystyle \frac{AE}{BE}=\frac{AC}{BC}.$
By the Thales' theorem, $\displaystyle \frac{BD}{BC}=\frac{AF}{AC}=\frac{AD}{AC},\,$ i.e., $\displaystyle \frac{AD}{BD}=\frac{AC}{BC},\,$ implying $\displaystyle \frac{AD}{BD}=\frac{AE}{BE}.\,$
By the converse of the Internal Angle Theorem, $DE\,$ is an angle bisector in $\Delta ABD\,$ and so is $AZ.\,$ Thus $\angle DAZ=30^{\circ}.$
Acknowledgment
This is A Problem from the 1985 Balkan Mathematical Olympiad (Shortlist). The problem has been proposed by Dimitris Kontogiannis. It was originally posted at the Romantics of Geometry (Οι Ρομαντικοι της Γεωμετριας) facebook page. Solution 1 is by Leo Giuguic; Solution 2 by Benjamin Leis.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73549489
