BMO 2014, Problem 3
What Might This Be About?
Problem
Let $ABCD$ be a trapezium inscribed in a circle $\Gamma$ with diameter $AB.$ Let $E$ be the intersection point of the diagonals $AC$ and $BD.$ The circle with center $B$ and radius $BE$ meets $\Gamma$ at the points $K$ and $L,$ where $K$ is on the same side of $AB$ as $C.$ The line perpendicular to $BD$ at $E$ intersects $CD$ at $M.$
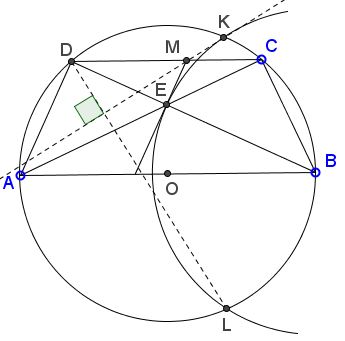
Prove that $KM$ is perpendicular to $DL.$
Solution 1
Since $AB\parallel CD,$ we have that $ABCD$ is isosceles trapezoid. Let $O$ be the center of $\Gamma$ and $EM$ meets $AB$ at point $Q.$ Then, from the right angled triangle $BEQ,$ we have $BE^{2} = BO\cdot BQ.$ Since $BE = BK,$ we get
(1)
$BK^{2} = BO\cdot BQ.$
Suppose that $KL$ meets $AB$ at $P.$ Then, from the right angled triangle $BAK,$ we have
(2)
$BK^{2} = BP\cdot BA.$
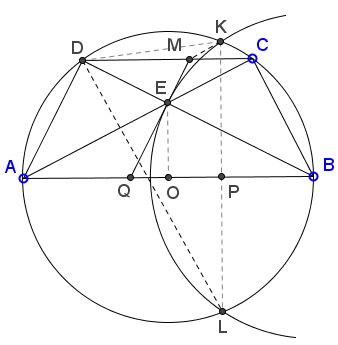
From (1) and (2) we get $\displaystyle \frac{BP}{BQ} =\frac{BO}{BA} =\frac{1}{2},$ and therefore $P$ is the midpoint of $BQ:$
(3)
$BP=PQ.$
However, $DM\parallel AQ$ and $MQ\parallel AD$ (both are perpendicular to $DB).$ Hence, $AQMD$ is parallelogram and thus $MQ = AD = BC.$ We conclude that $QBCM$ is isosceles trapezoid. It follows from (3) that $KL$ is the perpendicular bisector of $BQ$ and $CM,$ that is, $M$ is symmetric to $C$ with respect to $KL.$ Finally, we get that $M$ is the orthocenter of $\Delta DLK$ by using the well-known result that the reflection of the orthocenter of a triangle to every side belongs to the circumcircle of the triangle and vise versa.
Solution 2
Let $\Gamma$ be described by the equation $x^2+y^2=1$ and assume the vertices are given as $A(-1,0),$ $B(1,0),$ $C(\cos 2t, \sin 2t)$ and $D(-\cos 2t, \sin 2t),$ $t\in(0,\pi /4).$ This, in particular, means that $\angle BOC=2t,$ whereas $\angle BAC=t.$ From here, the slope of $AC$ equals $\tan t$ such that $AC$ is defined by the equation $y=\tan t\cdot (x+1),$ which for $x=0,$ gives $y=\tan t,$ implying $E=(0,\tan t).$
The square of the distance between $B$ and $E$ is
$\displaystyle BE^{2}=1^{2}+\tan^{2}t=\frac{1}{\cos^{2}t}=\frac{2}{1+\cos 2t}.$
This gives the equation of circle $C(B,E)$ as $(x-1)^2+y^2=2/(1+\cos 2t),$ wherefrom
$\displaystyle K=\bigg(\frac{\cos 2t}{1+\cos 2t}, \frac{\sqrt{1+2\cos 2t}}{1+\cos 2t}\bigg)$ and $\displaystyle L=\bigg(\frac{\cos 2t}{1+\cos 2t}, -\frac{\sqrt{1+2\cos 2t}}{1+\cos 2t}\bigg).$
The equation of the tangent at $E$ to $C(B,E)$ is $y-\tan t=x \cot t.$ It intersects $CD$ at $\displaystyle M=\bigg(\cos 2t \frac{1-\cos 2t}{1+\cos 2t},\sin2t\bigg).$ Now it is easy to verify that the product of slopes $MK$ and $DL$ is $-1.$
Acknowledgment
This is Problem 3 from the XXXI Balkan Mathematical Olympiad. I am grateful to Leo Giugiuc for communicating the problem and the second solution.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73584028
