The Midpoint of an Angle Bisector - a Problem by A. A. Zaslavsky
What Is This About?
Problem
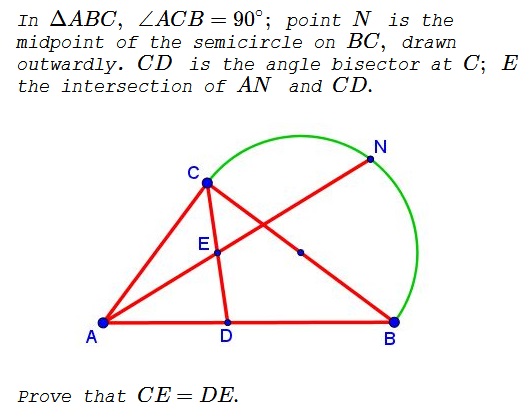
Solution
Let $F\,$ be the midpoint of $BC.\,$ WLOG, we can choose, $F=(0,0);\,$ $A=(-a,-b);\,$ $B(a,b);\,$ $C=(-a,b).\,$ Then, $N=(0,a+b)\,$ and the midpoint of $G\,$ of $BC\,$ becomes $G=(0,b).\,$ Let $I=(-a-b,0)\,$ and $K\,$ be the midpoints of the semicircles drawn outwardly on $AC\,$ and $AB,\,$ respectively. The bisector $CD\,$ passes through $K\,$ and, by Kiepert's Theorem, the lines $AN,\,$ $BI,\,$ $CK\,$ are concurrent at, say, $E.$
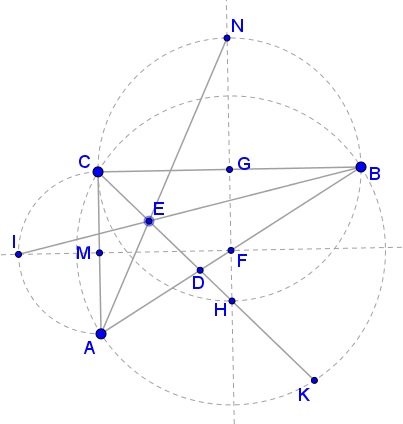
Since $\angle DCB=45^{\circ},\,$ $CD\,$ also passes through $H,\,$ the antipode of $N\,$ on the circle $(G).\,$ $H=(0,b-a).$
We can easily find the equations of the following lines:
$\displaystyle \begin{cases} BI: & y=\frac{b(a+b+x)}{2a+b}\\ CH: & y=b-a-x\\ AN: & y=a+b-\frac{a+2b}{a}x. \end{cases}$
The three indeed intersect at point $\displaystyle E=\left(-\frac{a^2}{a+b},\frac{b^2}{a+b}\right).$ Now, the midpoint of $AC\,$ is, say, $M=(-a,0)\,$ whereas the midpoint of $BC\,$ is $G=(0,b).\,$ The midline $MG\,$ is defined by $ab+bx=ay\,$ and we can verify that $E\,$ lies on $MG.$ It follows that $CE=DE.$
Acknowledgment
The problem is due to A. A. Zaslavsky. I found it at the facebook page of Rovshan Pirkuliev.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73517913
