Concyclic Points at the IMO 2014
What is this about?
Problem 4, IMO 2014
Let $P$ and $Q$ be on segment $BC$ of an acute triangle $ABC$ such that $\angle PAB=\angle BCA$ and $\angle CAQ=\angle ABC$. Let $M$ and $N$ be the points on $AP$ and $AQ$, respectively, such that $P$ is the midpoint of $AM$ and $Q$ is the midpoint of $AN$.
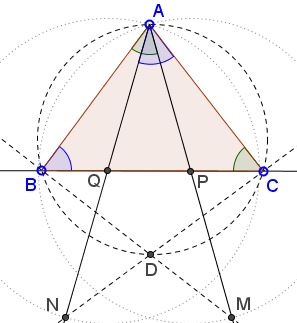
Prove that the intersection $D$ of $BM$ and $CN$ is on the circumference of triangle $ABC$.
Complex Numbers
We shall treat points in the plane as complex numbers and use the same notation for both.
Triangles $ABC$ and $PBA$ are similar, with different orientations, implying
(1)
$\displaystyle\frac{A-P}{B-P}=\bigg(\frac{C-A}{B-A}\bigg)^{*}.$
Where the asterisk denotes complex conjugation. Similarly, $\Delta ACB\sim\Delta QCA$ so that
(2)
$\displaystyle\frac{C-Q}{A-Q}=\bigg(\frac{C-A}{B-A}\bigg)^{*}.$
But
(3)
$\begin{align} M-P&=-(A-P),\\ N-Q&=-(A-Q). \end{align}$
Combining (1), (2), (3) gives
$\displaystyle\frac{M-P}{B-P}=\frac{C-Q}{N-Q},$
implying that triangles $MPB$ and $CQN$ are similar. Now it is obvious that $\angle ABM+\angle ACN=\pi,$ so that quadrilateral $ABDC$ is indeed cyclic.
Analytic Geometry
Choose the Cartesian coordinates so that $A=(0,2),$ $B=(-2b,0),$ $C=(2c,0).$ Then $b=\cot B$ and $c=\cot C.$ From these,
$\displaystyle\cot A=-\cot(B+C)=\frac{1-bc}{b+c}.$
Let $P=(2p,0),$ with $p\in(-b,c).$
In $\Delta APB,$ $\angle APB=A$ and $p=\cot\angle APB,$ implying $\displaystyle p=\frac{1-bc}{b+c},$ which delivers $\displaystyle P=(2\frac{1-bc}{b+c},0).$ Similarly, $\displaystyle Q=(-2\frac{1-bc}{b+c},0).$ By the construction, $\displaystyle P=(4\frac{1-bc}{b+c},-2)$ and $\displaystyle N=(-4\frac{1-bc}{b+c},-2).$
The equation of $BM$ is $\displaystyle x=-2b-\bigg(b+2\frac{1-bc}{b+c}\bigg)y;\,$ that of the circumcircle $(ABC)$ is
$[x=(c-b)]^{2}+[y-(1-bc)]^{2}=(1+b^{2})(1+c^{2}).$
By straightforward calculations, the second intersection of the two is
$\displaystyle D=\bigg(2\frac{(c-b)(2-bc)}{(c-b)^{2}+4},-2\frac{(c+b)^{2}}{(c-b)^{2}+4}\bigg).$
Since this expression is symmetric in $b$ and $c,$ $D$ is also the intersection of $CQ$ with the circumcircle and so $D=BM\cap CQ$ and lies on the circle.
Euclidean Geometry
This could be considered as a synthetic interpretation of the solution in complex numbers
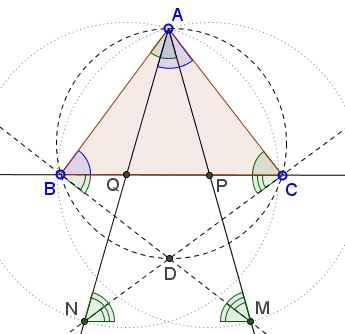
By simple angle chasing, $\angle APB=\angle AQC=\angle BAC\,$ such that triangles $ABP$ and $CAQ$ have the same angles and are, therefore, similar:
$\displaystyle\frac{BP}{AP}=\frac{CQ}{AQ}.$
By the construction, $MP=AP$ and $NQ=AQ$ so that also
$\displaystyle\frac{BP}{MP}=\frac{CQ}{NQ}.$
Since $\angle BPM=180^{\circ}-\angle APB$ and $\angle NQC=180^{\circ}-\angle AQC,$ we also have $\angle BPM= \angle NQC,$ making triangles $BPM$ and $NQC$ similar. Now, say
$\begin{align} \angle BAC = \angle AQP &= \angle ANM\\ &=\angle QNC+\angle MNC\\ &=\angle MBC+\angle NCB\\ &=\angle DBC+\angle DCB\\ &=180^{\circ}-\angle BDC, \end{align}$
so that $\angle BAC+\angle BDC=\pi,\,$ and the quadrilateral $ABDC$ is indeed cyclic.
Note: $D$ lies on the circumcircle of $\Delta ABC\,$ regardless whether it is acute or not. It does not appear that this condition may affect the solution in any way.
Acknowledgment
The solutions in complex numbers and analytic geometry are due to Leo Giugiuc (Romania).
What Can Be Multiplied?
- What Is Multiplication?
- Multiplication of Equations
- Multiplication of Functions
- Multiplication of Matrices
- Multiplication of Numbers
- Peg Solitaire and Group Theory
- Multiplication of Permutations
- Multiplication of Sets
- Multiplication of Vectors
- Multiplication of a Vector by a Matrix
- Vector Space and Spaces with the Scalar Product
- Addition and Multiplication Tables in Various Bases
- Multiplication of Points on a Circle
- Multiplication of Points on an Ellipse
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73510427
