A Problem That Fermat Might Have Liked
Problem
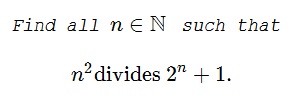
Solution
We shall depend on Fermat's Little Theorem:
For a prime $p\,$ and for $a\in\mathbb{N}\,$ coprime to $p,\,$ $p\,$ divides $a^{p-1}-1.$
Assume first $n\,$ is prime, $n=p.\,$ Clearly, $p\,$ ought to be odd. Then $2^p+1=(2^{p-1}-1)+(2^{p-1}-1)+3.\,$ Since, by Fermat's Little Theorem, $p\,$ divides $2^{p-1}-1\,$ and, assuming $p\,$ divides $2^p+1,\,$ $p\,$ divides $3\,$ and, therefore, $p=3.\,$ We easily check that $p=3\,$ solves the problem and is the only prime that does that.
Assume now that $n=px,\,$ where $p\,$ is an odd prime and $x\,$ a natural number, $x\gt 1.\,$ Then
$\displaystyle\begin{align} 2^n+1 &= 2^{px}+1 = 2^{(x-1)p+p}+1=2^p\cdot (2^p)^{x-1}+1\\ &=\underbrace{\left((2^p)^{x-1}-2^{x-1}\right)+\ldots+\left((2^p)^{x-1}-2^{x-1}\right)}_{2^p\text{ times}}+(2^{p(x-1)}+1). \end{align}$
Now, for natural $a,b,m,\,$ $(a-b)|(a^m-b^m)\,$ so that $(2^p-2)|((2^p)^{x-1}-2^{x-1})\,$ and, consequently, $p|((2^p)^{x-1}-2^{x-1}).\,$ Since, by our assumption, $p|(2^n+1),\,$ $p|(2^{p(x-1)}+1).\,$ Taking the difference gives that $p$ divides $2^{px}-2^{p(x-1)}=2^{p(x-1)}(2^p-1).$ In other words, $p|(2^p-1).$ But $2^p-1=2(2^{p-1}-1)+1,\,$ implying that $p|1.$ A contradiction.
Acknowledgment
The problem has been proposed by Lorenzo Villa on twitter.com as an example of a number theoretic brainteasers that P. Fermat would have particularly loved.
![]()
|Contact| |Up| |Front page| |Contents| |Arithmetic|
Copyright © 1996-2018 Alexander Bogomolny73573756
