When Two Segments Intersect?
Problem
Given two segments in the plane, $P_{1}P_{2}$ and $Q_{1}Q_{2}.$ Specify a condition that insures that the two segments intersect.
Solution
The two segments define two lines, say, $xa_{i}+yb_{i}+c_{i}=0,\space i=1,2.$ The lines may or may not intersect. If they do not, neither do the segments. However, the segments may not intersect even when the lines do:
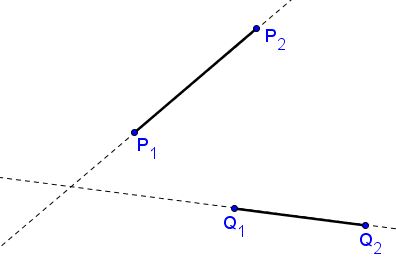
So finding the intersection of two lines would not solve the problem at hand. Nonetheless, the diagram may point us in the right direction. Let's first consider what might be a simpler problem. It should be simpler to check when a segment intersects a line:

Given a line $xa+yb+c=0$ and a segment in the plane, $P_{1}P_{2}.$ Specify a condition that insures that the segment intersects the line.
The answer to this question is rather obvious: a segment intersects a line provided its end points lie on different sides of the line. (I ignore the possibility that the segment lies on the line.) How do we know when this happens?
A line $L(x,y)=xa+yb+c=0$ separates the plane into two half-planes: $\{(x,y):\space L(x,y)\gt 0\}$ and $\{(x,y):\space L(x,y)\lt 0\}$. It separates two points $P_{1}$ and $P_{2}$ if they lie in different half-planes defined by the line: for one $L(x,y)$ is positive, for the other, it's negative, i.e., when
$L(P_{1})L(P_{2})\lt 0.$
Returning to the initial problem, let $L_{p}(x,y)=0$ and $L_{q}(x,y)=0$ be the equation of the lines which carry segments $P_{1}P_{2}$ and $Q_{1}Q_{2},$ respectively. For the segments to intersect, one's end points need to be separated by the line defined by the other.
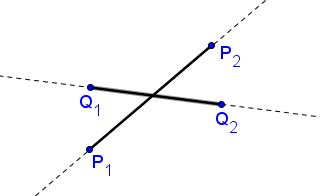
This happens when
$L_{q}(P_{1})L_{q}(P_{2})\lt 0$ and $L_{p}(Q_{1})L_{p}(Q_{2})\lt 0.$
Note: thes condition has been used on the Voronoi Diagram page to determine whether the edges of the Voronoi diagram and those of its dual intersect or not.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73614753
