A Property of Product of Special Matrices, Probably Folklore
Problem
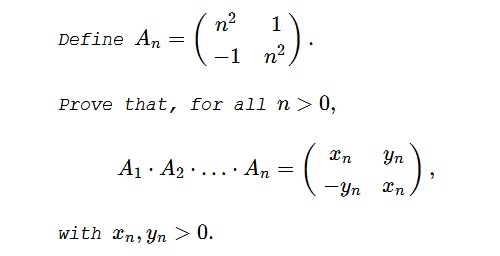
Solution 1
For all integer $k\ge 1,$
$\displaystyle A_k=\sqrt{k^4+1}\left(\begin{array}{cc}\cos (\arctan\frac{1}{k^2})&\sin(\arctan\frac{1}{k^2})\\-\sin(\arctan\frac{1}{k^2})&\cos(\arctan\frac{1}{k^2})\end{array}\right).$
Thus
$\displaystyle \prod_{k=1}^nA_k=\left(\prod_{k=1}^n\sqrt{k^4+1}\right)\left(\begin{array}{cc}\cos \left(\displaystyle \sum_{k=1}^n\arctan\frac{1}{k^2}\right)&\sin\left(\displaystyle \sum_{k=1}^n\arctan\frac{1}{k^2}\right)\\-\sin\left(\displaystyle \sum_{k=1}^n\arctan\frac{1}{k^2}\right)&\cos\left(\displaystyle \sum_{k=1}^n\arctan\frac{1}{k^2}\right)\end{array}\right).$
Now observe that, for $k\ge 1,$ $\displaystyle \frac{1}{k^2}\le\frac{1}{k^2-k+1}.$ But $\displaystyle 0\lt\arctan (k)-\arctan (k-1)\lt\frac{\pi}{2}.$ And $\displaystyle \arctan (k)-\arctan (k-1)=\frac{1}{k^2-k+1}.$ Thus it follows that
$\displaystyle \arctan (k)-\arctan (k-1)=\arctan\left(\frac{1}{k^2-k+1}\right).$
Putting everything together,
$\displaystyle \begin{align} \sum_{k=1}^n\arctan \frac{1}{k^2} &\le \sum_{k=1}{n}\arctan\left(\frac{1}{k^2-k+1}\right)\\ &=\sum_{k=1}^n(\arctan (k)-\arctan (k-1)\\ &=\arctan (n)\lt\frac{\pi}{2}, \end{align}$
proving the result.
Solution 2
Matrices $\displaystyle M(a,b) := \begin{pmatrix} a & b \\ -b & a \end{pmatrix}$ correspond to complex numbers $a+ib$ and the map $ a+ib \mapsto M(a,b)$ is in fact a isomorphism of rings. So for all intents and purposes, $M(a,b)$ and $a+ib$ are the same thing.
Thus, we may rewrite in polar coordinates
$\displaystyle A_k = k^2 + i = \sqrt{k^4+1}\;e^{i\arctan(1/k^2)} $
and
$\displaystyle \prod_{k=1}^n A_k = \left(\prod_{k=1}^n \sqrt{k^4+1}\right)\exp(i\sum_{k=1}^n \arctan(1/k^2))$
Now we need to show that the angle $\displaystyle \sum_{k=1}^n \arctan(1/k^2)$ lies in the interval $ (0,\pi/2)$. This just means that the product $\displaystyle \prod_{k=1}^n A_k $ lies in the positive quadrant. It is clear that the angle is greater than $ 0 $. To find an upper bound, we could try to use $ \arctan(x) \leq x $ for nonnegative $ x $:$\displaystyle \sum_{k=1}^n \arctan(1/k^2) \leq \sum_{k=1}^\infty \frac{1}{k^2} = \frac{\pi^2}{6} $
The last equality is pretty well-known as solution to the Basel problem. Sadly $ \pi/2 \simeq 1.57 $ and $ \pi^2/6 \simeq 1.64 $. To get a more accurate bound, we can try to use additional terms of the Taylor expansion of $ \arctan $:
$\displaystyle \arctan(x) \leq x - x^3/3 + x^5/5 \qquad \text{ for } x \geq 0 $
In the next step we will use
$\displaystyle \sum_{k=1}^\infty 1/k^6 = \frac{\pi^6}{945} \qquad \sum_{k=1}^\infty 1/k^{10} = \frac{\pi^{10}}{93555}$
We actually don't need the precise values and could theoretically use (good enough) approximations instead.
$\displaystyle \begin{align} \sum_{k=1}^n \arctan(1/k^2) \leq& \sum_{k=1}^\infty \frac{1}{k^2} - \frac{1}{3k^6} + \frac{1}{5k^{10}} \\=& \frac{\pi^2}{6} - \frac{\pi^6}{3\cdot 945} + \frac{\pi^{10}}{5\cdot 93555} \\\simeq& 1.51 \lt \pi/2 \end{align}$
Solution 3
Write $A_n=n^2+i,$ a complex number. $A_n$ has argumnet $\displaystyle \theta_n:\,\tan\theta_n=\frac{1}{n^2},$ $n\ge 1.$
To insure that the product $A_1A_2\ldots A_N$ lies in the frist quadrant, we need to have
$\displaystyle \sum_{n=1}^N\theta_n\lt\frac{\pi}{2},$
or,
$\displaystyle \sum_{n=2}^N\theta_n\lt\frac{\pi}{4},$since $\displaystyle \theta_1=\frac{\pi}{4}.$ Now, using $\arctan (x)\lt x,$ for $x\gt 0,$
$\displaystyle\begin{align}\sum_{n=2}^N\theta_n&=\sum_{n=2}^N\arctan \left(\frac{1}{n^2}\right)\\ &\lt\sum_{n=2}^N\frac{1}{n^2}\lt\sum_{n=2}^{\infty}\frac{1}{n^2}=\sum_{n=1}^{\infty}\frac{1}{n^2}-1=\frac{\pi^2}{6}-1\\ &\lt\frac{\pi}{4},\end{align}$
since $\displaystyle \frac{\pi^2}{6}\lt 1+\frac{\pi}{4}.$
Acknowledgment
The problem, with a solution, was kindly communicated to me by Leo Giugiuc. Leo noted that, in all likelihood, the problem is part of mathematical folklore. Solution 1 is Leo's; Solution 2 is by Long Huynh Huu; Solution 3 is by Sam Walters.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73518359
