Leibniz and Pascal Triangles

The applet below presents Pascal and Leibniz triangles modulo a specified number. (In addition, all entries exceeding 10 are displayed modulo 10. Also, for the Leibniz triangle whose entries are unit fractions, i.e. fraction with 1 in the numerator, we use their whole reciprocals.)

The Pascal Triangle is a standard fixture in recreational mathematics. Formed by binomial coefficients it possesses an inordinate number of interesting properties (see the references below.) Its construction starts from the top. In every row, the first and the last numbers equal 1. A generic entry is obtained by summing up the two entries just above it.

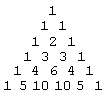
The Leibniz Triangle [Polya, p 88], also called the Leibniz Harmonic Triangle, is by far less known, although it relates to that of Pascal in a very simple way.

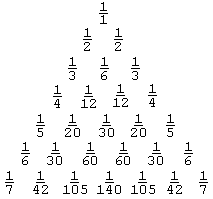
A row of the Leibniz triangle starts with the reciprocal of the row number (or the row number plus one depending on whether one starts counting from 1 or 0.) Every entry is the sum of the two numbers just below it. The entries can thus be computed sequentially left to right and top to bottom using subtraction instead of addition. E.g., in the fifth row, 1/20 = 1/4 - 1/5, 1/30 = 1/12 - 1/20, 1/20 = 1/12 - 1/30, 1/5 = 1/4 - 1/20. Asymmetry of construction notwithstanding, the triangle is symmetric with respect to its vertical axis.

in which all the terms eventually cancel out except for the very first, thus giving the sum of 1. (There is a geometric illustration for the telescoping series.) It appears that the first term in the first row is the sum of the second terms from all rows starting with the second one. This property is generalized: the last term in the n^th row is the sum of the (n+1)-st terms from all the rows starting with the (n+1)-st. E.g.,

m^th element in the n^th row of the Pascal triangle equals the binomial coefficient C(n,m), where we start counting from 0. The corresponding entry of the Leibniz triangle is the reciprocal of (n+1)C(n,m). (In particular, it can be verified that the reciprocals of (n+1)C(n,m) and (n+1)C(n,m+1) add up to the reciprocal of nC(n-1,m).)

References

1. R.Graham, D.Knuth, O.Patashnik, Concrete Mathematics, 2nd edition, Addison-Wesley, 1994
2. H.E.Huntley, The Divine Proportion, Dover, 1970
3. J.A.Paulos, Beyond Numeracy, Vintage Books, 1992
4. C.A.Pickover, Computers, Patterns, Chaos, and Beauty, St. Martin's Press, 1990
5. G.Polya, Mathematical Discovery, Wiley, 1981
6. I.Stewart, Game, Set and Math, Penguin Books, 1989
7. D.Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Books, 1987
8. D.Wells, You Are a Mathematician, Wiley, 1995