For $n \ge 1,$ $\displaystyle 2(\sqrt{n}-\sqrt{n-1})\gt\frac{1}{\sqrt{n}}$

The motivation for this page came from a challenge issued by Steven Strogatz in an October 6, 2015, tweet and one elegant (trigonometric) solution submitted as a response.

My students found three ways to show 2[sqrt(n) - sqrt(n-1)] > 1/sqrt(n). Can you? Hint: Use algebra, calculus, & calculus + geometry

Prove that for integer $n \ge 1,$ $\displaystyle 2(\sqrt{n}-\sqrt{n-1})\gt\frac{1}{\sqrt{n}}.$

Multiply the left-hand side by $\displaystyle\frac{\sqrt{n}+\sqrt{n-1}}{\sqrt{n}+\sqrt{n-1}}.$ The problem is equivalent to proving

$\displaystyle\frac{2}{\sqrt{n}+\sqrt{n-1}}\gt\frac{1}{\sqrt{n}}.$

But obviously,

$\displaystyle\frac{2}{\sqrt{n}+\sqrt{n-1}}\gt\frac{2}{2\sqrt{n}}\gt\frac{1}{\sqrt{n}}.$

Multiply both sides by $\sqrt{n}(\sqrt{n}+\sqrt{n-1}).$ The problem is equivalent to proving

$2(n^2-n(n-1))\gt n+\sqrt{n(n-1)}.$

But $n^2-n(n-1)=n$ and obviously $n\gt\sqrt{n(n-1)}$ so that

$2(n^2-n(n-1))\gt 2n\gt n+\sqrt{n(n-1)}.$

As in the first solution, multiply the left-hand side by $\displaystyle\frac{\sqrt{n}+\sqrt{n-1}}{\sqrt{n}+\sqrt{n-1}},$ then move to the reciprocals. The problem is equivalent to proving

$\displaystyle\frac{\sqrt{n}+\sqrt{n-1}}{2}\lt\sqrt{n},$

I.e., $\sqrt{n-1}\lt\sqrt{n}$ which is obvious.

By the AM-GM inequality,

$\displaystyle\frac{n+(n-1)}{2}\gt\sqrt{n(n-1)}.$

Divide this by $\sqrt{n}$ and multiply by $2:$

$\displaystyle 2\sqrt{n}-\frac{1}{\sqrt{n}}\gt 2\sqrt{n-1}.$

This is equivalent to the required inequality.

This solution is by Mike Lawler.

Consider the right triangle

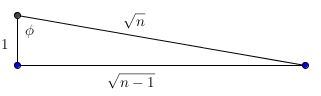
Observe that $\displaystyle\cos\phi=\frac{1}{\sqrt{n}},$ $\displaystyle\sin\phi=\frac{\sqrt{n-1}}{\sqrt{n}}$ and $\tan\phi=\sqrt{n-1}.$ Thus the required inequality is equivalent to

$\displaystyle 2\left(\frac{1}{\cos\phi}-\frac{\sin\phi}{\cos\phi}\right)\gt\cos\phi.$

This transforms into

$2(1-\sin\phi)\gt\cos^{2}\phi = 1-\sin^{2}\phi$

and, finally, into

$(1-\sin\phi)^{2}\gt 0$

which is true.

The Taylor series of function $f(x)=\sqrt{1-x}$ around $x=0$ is easily seen to equal

$\displaystyle\sqrt{1-x}=1-\frac{x}{2}-\frac{x^2}{8}-\frac{x^3}{16}-\frac{5x^4}{128}-\ldots$

Importantly, all coefficients in series but the first one are negative such that, for $x\gt 0,$ $\displaystyle\sqrt{1-x}\lt 1-\frac{x}{2}.$ To make use of that, divide the two sides of the required inequality by $\sqrt{n}:$

$\displaystyle 2\left(1-\sqrt{1-\frac{1}{n}}\right)\gt\frac{1}{n}.$

However, due to the previous remark,

$\displaystyle 2\left(1-\sqrt{1-\frac{1}{n}}\right) \gt 2\left(1-\left(1-\frac{1}{2n}\right)\right) =\frac{1}{n},$

as required.

Consider integral $\displaystyle\int_{n-1}^{n}\frac{dx}{\sqrt{x}}=2(\sqrt{n}-\sqrt{n-1}).$ That the integral exceeds the area of the rectangle in the diagram below is rather obvious.

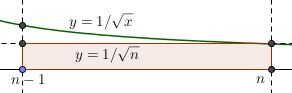
It may also be argued that the function $\displaystyle f(x)=\frac{1}{\sqrt{x}}$ is strictly decreasing for $x\gt 0;$ in particular, for $x\in [n-1,n),$ $\displaystyle f(x)\gt\frac{1}{\sqrt{n}},$ implying

$\displaystyle 2(\sqrt{n}-\sqrt{n-1})=\int_{n-1}^{n}\frac{dx}{\sqrt{x}}\gt\int_{n-1}^{n}\frac{dx}{\sqrt{n}}=\frac{1}{\sqrt{n}}.$

Perhaps perverse, but we may start with estimating the integral $\displaystyle\int_{n-1}^{n}\frac{dx}{\sqrt{x}}=2(\sqrt{n}-\sqrt{n-1})$ from above:

$\displaystyle\frac{1}{\sqrt{n-1}}\gt 2(\sqrt{n}-\sqrt{n-1}).$

Multiply this by $\displaystyle\frac{\sqrt{n-1}}{\sqrt{n}}$ to obtain

$\displaystyle\frac{1}{\sqrt{n}}\gt 2(\sqrt{n-1}-\frac{n-1}{\sqrt{n}})=2(\sqrt{n-1}-\sqrt{n}+\frac{1}{\sqrt{n}}).$

Rearranging terms leads to the required inequality.

This proof has been suggested by Steven Strogatz.

Apply the Mean Value Theorem to the function $f(x)=\sqrt{x}:$ there exists $c\in (n-1,n)$ such that $f(n)-f(n-1)=f'(c),$ i.e., $\displaystyle \sqrt{n}-\sqrt{n-1}=\frac{1}{2\sqrt{c}}.$ Since, $\displaystyle \frac{1}{\sqrt{x}}$ is decreasing on $[n-1,n],$ this implies

$\displaystyle \sqrt{n}-\sqrt{n-1}==\frac{1}{2\sqrt{c}}\gt\frac{1}{2\sqrt{n}}.$

This proof is by Grégoire Nicollier.

The curve $y = f(x) = \sqrt x$ is concave. The chord between the curve points of abscissae $x-1$ and $x$ is thus steeper that the tangent at $x:$ $f(x)-f(x-1)\gt f'(x)$ for all $x\ge 1.$