Problem 2 from the 2017 IMO
Problem
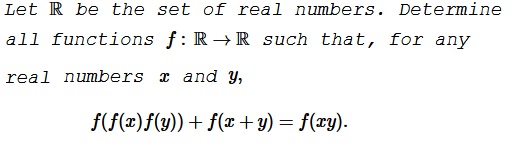
Solution
As is common, let $y=0:\,$ $f(f(x)f(0))+f(x)=f(0).\,$ Let $f(0)=k.\,$ We have $f(kf(x))+f(x)=k.\,$ Note in passing that $f(k^2)=0.$
If $k=0,\,$ then $f(0)+f(x)=k,\,$ implying $f(x)\equiv 0.\,$ So, assume $k\ne 0.\,$ Setting $f(x)=y\,$ gives
(1)
$f(ky)+y=k,$
or $\displaystyle f(y)=k-\frac{y}{k}.\,$ The question is now to find $k.\,$ Let's substitute this $f\,$ into the original equation with $x=y:$
$\displaystyle f\left(\left[k-\frac{x}{k}\right]^2\right)+\left(k-\frac{2x}{k}\right)=k-\frac{x^2}{k}.$
To complete the substitution,
$\displaystyle k-\frac{\displaystyle \left[k-\frac{x}{k}\right]^2}{k}-\frac{2x}{k}=-\frac{x^2}{k}.$
This reduces to
$\displaystyle k-\left(k-\frac{2x}{k}+\frac{x^2}{k^3}\right)-\frac{2x}{k}=-\frac{x^2}{k}$
and, further,
(2)
$\displaystyle x^2\left(\frac{1}{k^3}-\frac{1}{k}\right)=0,\,$ for all $x\in\mathbb{R},\,$
making $k(k^2-1)=0\,$ so that $k=\pm 1.$
There are three functions: $f(x)=0,\,$ $f(x)=x-1,\,$ $f(x)=1-x.$
Analysis
The weak point in the solution is the replacement of $f(x)\,$ with $y\,$ in the derivation of (1). Later on, we assert that (2) holds for all $x\in\mathbb{R},\,$ which is unwarranted, because (1) may be a priori claimed only for $y\,$ in the image $Im(f)\,$ of $f,\,$ i.e., for $y\,$ for which there is $x\,$ with $y=f(x).$
However, to obtain the desired conclusion from (2), it only necessary to exhibit a single $x\in Im(f)\,$ which is not $0.\,$ $k=f(0)\,$ is the first that comes to mind. But there are more. To remind, $f(k^2)=0.\,$ Setting $y=k^2\,$ in the original equation gives $f(0)+f(x+k^2)=f(k^2x),\,$ i.e., $k+f(x^2+k)=f(k^2x)\,$ from which, with $x=1,\,$ $f(k+1)=-k,\,$ which is also not zero. Thus we can rightfully claim that $f(0)=\pm 1\,$ for any solution $f\,$ of the original functional equation. That is far from the final solution of the problem but shows that the prior derivation was not entirely useless.
Regardless of the choice $k=\pm 1,\,$ $f(1)=0,\,$ for any non-trivial solution of the original equation.
Second Attempt
Let's assume for definiteness' sake that $f(0)=1.\,$ This gives $f(f(1)f(x))+f(x+1)=f(x),\,$ i.e., $f(x+1)=f(x)-1,\,$ for all $x\in\mathbb{R}.\,$ By induction, $f(x+n)=f(x)-n$ and also $f(x-n)=f(x)+n.\,$ It would have been nice to invoke continuity and the Intermediate Value Theorem to claim $f'\text{s surjectivity}\,$ that would immediately solve the problem. But continuity is not stipulated and does not a priori follow from $f(x+1)=f(x)-1.\,$ Thus it is vital to derive the necessary properties directly from the original equation.
The essential distinction between $f(x+1)=f(x)-1\,$ and $f(f(x)f(y)) + f(x+y) = f(xy)$ is in the "second-order" term $f(f(x)f(y)).\,$ Assume it is zero. This happens, e.g., if $x+y=xy.\,$ I'd like to conclude that, for such $x,y\,$ $f(x)f(y)=1.\,$ This would be true if $f(t)=0\,$ implied $t=1.\,$ Assume this is not so and there is $x\ne 1,\,$ such that $f(x)=0.\,$ For that $x,\,$ find $y\,$ from $x+y=xy.\,$ Then, $1=f(0f(y))=0,\,$ a contradiction. Thus, there is only one solution to $f(x)=0,\,$ namely, $x=1.\,$ It follows that for every integer $n,\,$ there is only one solution to $f(x)=n\,$ which is $x=1-n.\,$
So, for the record, $x+y=xy\,$ implies $f(x)f(y)=1.\,$ Note that, incidentally, neither $x\,$ nor $y\,$ could be $1.$
We are getting the first glimpse of the possible continuity of $f:\,$ For $x=n+1,\,$ $y=\displaystyle \frac{n+1}{n}\,$ whereas $f(n+1)=-n,\,$ implying $\displaystyle f\left(\frac{n+1}{n}\right)=-\frac{1}{n}.\,$ This is reassuring, but we won't need it.
So, we found that $f(x)=1,$ only for $x=0.\,$ Assume $f(f(x)f(y))=1.\,$ There are two ways to achieve that: having one of $x,y\,$ equal $1,\,$ or finding $x,y\,$ such that $f(x+y)=f(xy)-1.\,$ Since $f(xy)-1)=f(xy+1),\,$ we may try finding $x,y\,$ from $x+y=xy+1.\,$ Naturally, the two ways are equivalent: one of the numbers $x,y\,$ that satisfy $x+y=xy+1,\,$ is necessarily $1.\,$ Strangely, this observation proves to be useful.
We'll show that any solution to the given problem is injective, or $1-1:\,$ $f(a)=f(b)\,$ implies $a=b.\,$ As we saw earlier, this is true for integer values. Now it is the turn of a more general statement. Given such $a\,$ and $b\,$ we may want to find $x\,$ and $y\,$ such that $a=x+y\,$ and $b=xy+1.\,$ If we succeed, then one of $x,y\,$ will be $1,\,$ implying, say, $a=x+1=x\cdot 1+1=b.$
How are we going to look for the pair $x,y?\,$ From $x+y=a\,$ and $xy=b-1,\,$ the pair should be the roots of the quadratic equation, $g(u)=u^2-au+(b-1)=0.\,$ For the roots to be real we need a non-negative discriminant: $D=a^2-4(b-1)\ge 0\,$ which may be not true from the outset. However, if $f(a)=f(b),\,$ then also $f(a+n)=f(b+n),\,$ for any $n\in\mathbb{Z}.\,$ This will convert the discriminant to $D(n)=(a+n)^2-4(b+n-1),\,$ which is assured of being positive for large $n.\,$ So, to sum up, for $f(a)=f(b),\,$ we can always find real $x,y,n\,$ so that $a+n=x+y\,$ and $b+n=xy+1\,$ and, since $f(a+n)=f(b+n),\,$ one of $x,y$ is $1,\,$ implying $a+n=b+n\,$ and subsequently, $a=b.\,$
The injectivity does not directly lead to the desired surjectivity, but it allows to use the "second-order" term, while getting rid of it when necessary.
Let's set in the original equation $y=0.\,$ Since $f(0)=1,\,$ we get $f(f(x))+f(x)=1.\,$ We continue, substituting $f(x)\,$ for $x\,$ and $y=0:\,$ $f(f(f(x)))+f(f(x))=1,\,$ or
$\begin{align} f(f(x))+f(x)&=1\\ 1&=f(f(f(x)))+f(f(x)). \end{align}$
Adding which gives $f(f(f(x)))=f(x)\,$ and, subsequently, from the already proved injectivity, $f(f(x))=x.\,$ Since $x\,$ is arbitrary, this proves the surjectivity of $f.\,$ Now, the initial argument applies to show that $f(x)=1-x.\,$
Acknowledgment
This is Problem 2 from the 2017 IMO. The problem has been posted by N. N. Taleb at twitter.com.
Sam Walters has discovered a weak point in the above argument, viz., (1) is only true for $y\in Im(f).\,$ He also offered an example of a function different from the three found above that satisfies (1) for $k=1:$
$\displaystyle f(x)=\begin{cases} 1-x, & x\in\mathbb{Q},\\ \frac{1}{2}, & x\in\mathbb{R}\setminus\mathbb{Q}. \end{cases}$
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73575225
