Factorial Divisibility
Problem
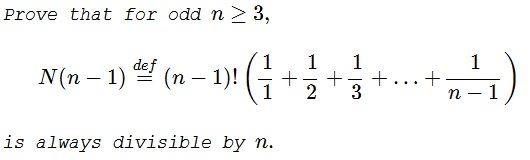
Solution 1
Observe that $\displaystyle \frac{1}{k}+\frac{1}{n-k}=\frac{n}{k(n-k)}.$ It follows that
$\displaystyle 2N(n-1)=n\cdot (n-1)!\left(\sum_{k=1}^{n-1}\frac{1}{k(n-k)}\right).$
Since $\displaystyle (n-1)!\left(\sum_{k=1}^{n-1}\frac{1}{k(n-k)}\right)$ is an integer, $2N(n-1)$ is indeed divisible by $n.$ And, since $n$ is odd, this is also true for $N(n-1).$
Solution 2
$\displaystyle\begin{align} T&=(n-1)!\sum_{k=1}^{n-1}\frac{1}{k}=(n-1)!\sum_{k=1}^{\frac{n-1}{2}}\left(\frac{1}{k}+\frac{1}{n-k}\right)=(n-1)!\sum_{k=1}^{\frac{n-1}{2}}\frac{n}{k(n-k)} \\ &=n\sum_{k=1}^{\frac{n-1}{2}}\frac{(n-1)!}{k(n-k)}. \end{align}$
For each term in the sum $k(n-k)|(n-1)!$ as $k$ and $n-k$ are distinct numbers in $\{1,2,...,n-1\}$. Thus, $n|T$.
Solution 3
If $n$ is prime then $\mathbb{Z}_{n}$ - the set $\{0, 1, 2,\ldots,n-1\}$ of the residues modulo $n$ is a field, with all elements bu $0,$ invertible. We may conclude that
$\displaystyle \sum_{k=1}^{n-1}\frac{1}{k}\equiv\sum_{k=1}^nk \text{mod } n\equiv 0\text{mod }n$
because $\displaystyle \sum_{k=1}^{n-1}=n\cdot\frac{n-1}{2}.$ Thus, for $n$ prime, $N(n-1)$ is divisible by $n.$
If $n$ is a composite odd, with a factor $m$ then in fact $m^2|(n-1)!$ because $m\lt n-1$ and $2m\le n-1.$ It then follows that each of the terms $\displaystyle \frac{(n-1)!}{k}$ is an integer divisible by $m.$ This is true for any factor of $n,$ $n/m$ in particular. We only need to choose $m$ mutually prime with $n/m$ to claim that every term $\displaystyle \frac{(n-1)!}{k}$ is divisible by $n.$
Acknowledgment
This is a problem from R. Honsberger's Mathematical Chestnuts from Around the World (MAA, 2001, pp 23-24.) The problem was originally offered at an East Germany Mathematical Olympiad for grades 11-12. A collection of olympiad problems was published in 1987 by former contestants.
Solution 2 is by Amit Itagi; Solution 3 is by Christopher D. Long. Christopher also made an observation that for some odd numbers (primes, in particular), $N(n-1)$ is divisible by $n^2.$
![]()
|Contact| |Up| |Front page| |Contents| |Arithmetic|
Copyright © 1996-2018 Alexander Bogomolny73580261
