|
|

|
|Store|
|

|

|

|
|

|

|

|

CTK Exchange
golland

guest
|
Sep-12-03, 11:47 PM (EST) |
|
|
"Geometry topic 205 continued"
| |
Hi Vladimir, I was and still am impressed by your construction solution involving hyperbola. Thanks for taking this problem to the very end. It is amazing how much geometry it was possible to squeeze out of a simple (at the first glance) problem.
One comment - if we had to resort to algebra ( AG ), then there
probably no need to transform the original hyperbola to normal.
the solution for the system of 2 equations ( linear and quadratic should be constructable. (?) G.
|
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
Vladimir
Member since Jun-22-03
|
Sep-14-03, 01:02 PM (EST) |
    |
1. "RE: Geometry topic 205 continued"
In response to message #0
| |
LAST EDITED ON Sep-16-03 AT 05:39 PM (EST)
Continuation of Geometry (The topics may get separated in the future.) You should have named this continuation Geometry Revisited.  It was a pleasure to work on this problem and, yes, I was also amazed how much geometry we squeezed out of it. In principle, it is not necessary to transform the hyperbola to a normal hyperbola by a parallel projection or by an affine transformation of the plane, in our case by a dilation of the plane along the vertical axis and rotation of the axes by -45º. We would get a quadratic equation in any plane and presence of the quadratic equation always indicates that the problem is constructible. But look at the hyperbola sketch in the X-Y coordinate system (X and Y axes coincident with the hyperbola primary and secondary axes). The equations of the given line l and of the original hyperbola are: X/s + Y/r = 1
X2/a2 - Y2/b2 = 1 where the lengths s = OS, r = OR, a = OA = OB, and b = OE = OF have already been constructed. Selecting the hyperbola primary axis a as the unit length a = 1 (it is always necessary to select a unit length for constructing products, ratios, and/or square roots of line seqments), we eliminate the coordinate Y of the desired point P Y = r - r/s·X = r·(1 - X/s)
Y2 = r2·(1 - 2X/s + X2/s2) Taking into account a = 1, we get the following quadratic equation for the coordinate X of the desired point P: X2 - r2/b2·(1 - 2X/s + X2/s2) = 1
(1 - r2/b2)·(X/s)2 - 2r2/b2·X/s - (1 + r2/b2) = 0 (X/s)2 + 2r2/b2/(1 - r2/b2)·X/s - (1 + r2/b2)/(1 - r2/b2) = 0 (X/s)2 + 2r2/(b2 - r2)·X/s - (b2 + r2)/(b2 - r2) = 0 Now the quadratic equation is substatntially more complex (and so would be the construction) and we would not even be solving for X but for the ratio X/s. As I recall the solution of the Cut the Triangle in Half problem - topic 248 in the High School Math forum, in that case I tried to transform the coordinate system in a way that would transform at least one of the 3 hidden hyperbolas (the one which was touching the desired line) into a normal hyperbola - not that I knew about the hyperbolas at the time - but the transformation only complicated the construction and so I refrained from using it. Possibly this was because we did not have a line given, but a point - and you do not simplify things but transforming a point, it'still has 2 coordinates and nothing has changed. Moreover, we really were not looking for a point on the hyperbola, the hyperbola was just hidden in the problem. However, the transformation simplified the subsequent analysis of the problem. Now if you want to see a really ugly quadratic equation, check the Bermuda Triangle problem - topic 373 in the College Math forum. That was my unfinished business from long ago. I returned to it right after solving the Cut the Triangle in Half problem, found some quadratic equation, but it was so complex that I did not even try the construction. I realized that there must be some special area and that the line solving the problem must touch its boundary, just like in the Cut the Triangle in Half problem, so I wanted to find the equation of the envelope of this family of lines. Well, even though I learnt the solution before I found the envelope, I found the envelope eventually. And it turned out to be a circle, i.e., something constructible with a compass. Anyway, the point is this: a quadratic equation always indicates that the problem is constructible, but solving it may not be the best way to get the solution, only if the quadratic equation is simple or if it can be transformed to a simple quadratic equation. For example, you have to find the signs of its coefficients, because the construction depends on it. Regards, Vladimir |
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
 |
golland

guest
|
Sep-14-03, 05:37 PM (EST) |
|
|
2. "RE: Geometry topic 205 continued"
In response to message #1
| |
Hi Vladimir, Parallel to posting "Cut triangle in half" on this site I also gave
it to some people I know. One of them came with the following
construction solution. For a given triangle ABC draw a bisector of angle A extended on
both sides of A. This is the main axis of the hyperbola.
Apollonius theorem states that any tangent to a hyperbola cutting
the sides of the angle A creates a triangle of invariant area.
It turns out that for this area to be 1/2 of the area ABC
the foci have to be SQRT( 1/2*b*c ) from A ( why ??) and
the tip of the hyperbola is SQRT( 1/2*p*(p-a) ) from A (why ??)
where a,b,c are the sides of the triangle, p=(a+b+c)/2. As you mention, the pedal curve for the other focus of the hyperbola (the one outside the ABC) is the circle touching the tip of hyperbola. So construction is simple : draw a circle using segment PF
as diameter (P - given point of cutting line, F - focus of hyperbola
on the extension of angle A bisector outside the triangle).
Draw a pedal circle. Out of 2 crossing points, select 1 and connect
to P and cut the triangle ABC. Simply beautiful!!!!! Do not say anything for a minute. Now, this possibly can be used to solve the other construction:
to find a point where the line crosses the hyperbola. The parameters
a and c of the hyperbola are given (say it is rectangular).
Now we have to find a point on the given line where segment of the
tangent line to hyperbola is cut in half. In a sence we have to
solve slightly modified problem of cutting triangle in 2, only this
time any triangle and any point P are OK as long as they do the job.
Any ideas on how to construct P and triangle for a given hyperbola? G.
|
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|
 |
Vladimir
Member since Jun-22-03
|
Sep-15-03, 06:39 PM (EST) |
    |
3. "RE: Apollonius' hyperbola"
In response to message #2
| |
LAST EDITED ON Sep-16-03 AT 04:18 PM (EST)
Given 2 lines b and c intersecting at a point A and making an angle a. Let points P and S slide on lines c and b, respectively, in such a way that the area S of the DAPS is constant. Lines PS are all tangents to a common hyperbola and we are going to prove it. 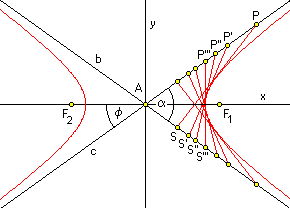
Select the x-y coordinate system with origin at the point A, the intersection of lines b and c, and x and y axes coincide with the agle bisectors of the 2 given lines. These angle bisectors are of course perpendicular to each other. Points P and S have coordinates P º (xP, yP)
S º (xS, yS) Since the points P and S are on the lines c and b, respectively, and since both lines pass through the origin A, we have yP = +xP·tanf
yS = -xS·tanf where f = a/2. The area S of the DAPS is S = 1/2·AP·AS·sina = 1/2·AP·AS·sin(2f) AP = Ö(xP2 + xP2) = xP·Ö(1 + tan2f) = xP/cosf
AS = Ö(xP2 + xS2) = xS·Ö(1 + tan2f) = xS/cosf S = 1/2·xP·xS·sin(2f)/cos2f = xP·xS·sinf·cosf/cos2f = xP·xS·tanf The equation of a line q passing through the points P and S is y - yS = (yP - yS)/(xP - xS)·(x - xS)
y + xS·tanf = (xP + xS)/(xP - xS)·tanf·(x - xS) Eliminating the x-coordinate of one point, say xP, we get xP = S/(xS·tanf)
y + xS·tanf = (S/(xS·tanf) + xS)/(S/(xS·tanf) - xS)·(x - xS)·tanf y + xS·tanf = (S + xS2·tanf)/(S - xS2·tanf)·(x - xS)·tanf This is an equation of a family of lines depending on a single parameter xS and we are going to find their envelope. Before we proceed, we express the equation as a quadratic equation for xS in order to simplify the subsequent calculation. (y + xS·tanf)·(S - xS2·tanf) = (S + xS2·tanf)·(x - xS)·tanf Multiplying this out, canceling identical terms, and rearranging the remaining terms according to the powers of xS we get xS2·(x + y)·tanf - 2xS·S·tanf + S·(x·tanf - y) = 0 This is the equation of our family of lines in the desired form F(x, y, xS) = 0. Equation of their envelope is given by ¶F/¶xS = 0: 2xS·(x + y)·tanf - 2S·tanf = 0
xS·(x + y) - S = 0
xS = S/(x + y) Eliminating the parameter xS from the equation F(x, y, xS) = 0 we get the equation of the envelope: S2/(x + y)2·(x + y)·tanf - 2S/(x + y)·S·tanf + S·(x·tanf - y) = 0 S·tanf - 2S·tanf + (x + y)·(x·tanf - y) = 0 x2·tanf - y2 = S·tanf x2/S - y2/(S·tanf) = 1 which is a hyperbola with the primary axis ÖS coincident with the coordinate x-axis (i.e., the bisector of the angle a), secondary axis Ö(S·tanf) coincident with the coordinate y-axis, the 2 given lines b and c as its asymptotes, and its 2 branches left and right of the origin A. Q.E.D. (to be continued) Now you ask why is it that for area S of the DAPS to be 1/2 of the area of the DABC, the focal points have to be Ö(1/2·b·c) from the vertex A and why the tip of the hyperbola is Ö(1/2·s·(s-a)) from the vertex A, where a, b, c are the sides of the DABC and s = (a + b + c)/2 its half-perimeter. Golland, you cannot just look at a given problem, you have to fiddle with it. What will happen when you change this and what will happen when you move that. Do you recall how I described moving the point P around the ellipse? I already know why (as a result of my fiddling for about 5 - 10 minutes) and I will tell you in my next post in a day or two. If you want to find out for yourself, start fiddling, you do not have much time. But that again, you do not need much time, the reasons are quite simple. Regards, Vladimir |
Attachments
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f6643483b0bdbfb.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f6643483b0bdbfb.gif
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|
 |
Golland

guest
|
Sep-16-03, 06:18 PM (EST) |
|
|
4. "RE: Apollonius' hyperbola"
In response to message #3
| |
Hello Vladimir, I do not quite understand the reasons behind your proofs here. The Apollonius theorem is a known fact (it is mentioned in Mathworld
in Hyperbola chapter and in many other sources, I guess). I am sure
that there are textbooks that have the complete proof of this theorem
in it's B.C. ( before calculus ) form. We are allowed to use this
and all other formulas and theorems liberally, even in cases when
we do not know or do not quite understand the inner workings of them
(mandatory knowledge of at least one of several possible proofs is
neither nessesary nor sufficient condition for usage). We do not have to prove that if y=x^2, then y'=2x every time
we take this derivative. My understanding is that this site is not a tutorial place. It is
a place where people can get help with difficult (for them) problems
and also a place where people can share some original and curious
math applications and ideas . What is so original or interesting in any other sense in the proof
itself that you posted? And why not to mention (and prove while you are at it) the fact that all segments PS are bisected by the point of touch with hyperbola? The outline of the original (without analitical geometry or calculus) proof would be much more interesting.
Now, the only questions I placed (in a challenge form) were the expressions for the a and c parameters of the hyperbola for a given triangle. I also pointed out a possible link of this construction to the construction problem of a crossing point of hyperbola and a
given line.
I did not ask for advice on how much time I should spend on the problem nor on how to proceed while in the process. G.
|
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|
 |
|
 |
|
 |
|
 |
Vladimir
Member since Jun-22-03
|
Sep-17-03, 08:12 PM (EST) |
    |
8. "RE: Apollonius' hyperbola"
In response to message #4
| |
LAST EDITED ON Nov-02-03 AT 06:15 PM (EST)
Hello Golland, > I do not quite understand the reasons behind your proofs here.
>
> The Apollonius theorem is a known fact (it is mentioned in
> Mathworld in Hyperbola chapter and in many other sources, I guess).
> I am sure that there are textbooks that have the complete proof of
> this theorem in it's B.C. ( before calculus ) form. We are allowed
> use this and all other formulas and theorems liberally, even in
> cases when we do not know or do not quite understand the inner
> workings of them (mandatory knowledge of at least one of several
> possible proofs is neither nessesary nor sufficient condition for
> usage).
>
> We do not have to prove that if y=x^2, then y'=2x every time
> we take this derivative. As opposed to taking simple derivatives, I have not seen Apollonius' theorem about hyperbola until recently (I did not do much geometry since high school). It is true that the theorem is mentioned on the Hyperbola page at MathWorld, but there is no proof. Before I feel entitled to use it, I want to see the proof and to understand it. If I cannot find somebody else's proof, I try to prove it myself. Let me give you an example from the book The History of Mathemathics: A Brief Course written by R. L. Cooke, Ph.D., emeritus professor of mathematics at the University of Vermont, and published by John Wiley, who is no huckleberry himself. In Chapter 6 we read: Exercise 6.16: At one point in his estimation of p Archimedes arrived at a rational approximation 591-1/8 : 153. Now the fraction 1/8 that occurs in this expression could actually be replaced by 1/7, and would yield a stronger estimate. Why do you think Archimedes prefers the weaker estimate with 1/8?
Solution: Undoubtedly 8 is much easier denominator to compute with that 7. The author has much better exercises. But a common reaction to the above one might be: Why not, Archimedes was a smart guy, everyone knows that. Until somebody (like me) goes ahead and actually types these numbers into the Windows calculator (let's see how close Archimedes got!): 591.125/153 = 3.863562 ... Huh?? Archimedes surely knew better than that - the next exercise deals with his rational approximation p » 22/7. Must be a typo. What are the correct numbers? Assuming at least one integer and the twice mentioned 1/8 are correct 153·p » 480.664
591.125/p » 188.161 Both estimates (591-1/8 : 188 and, say, 480-5/8 : 153) get worse when replacing 1/8 by 1/7, will not do. The most similar expression I can come up with is 32·153/3·519-1/2 = 3.141482 ... = (1 - 0.000035)·p Good, but where is the 1/8 or 1/7? What did the author have in mind? > ...
>
> What is so original or interesting in any other sense in the proof
> itself that you posted? I did not try to make an original proof, just a proof. > And why not to mention (and prove while you are at it) the fact
> that all segments PS are bisected by the point of touch with
> hyperbola? I was going to do that but I forgot. Nevertheless, for now, I do not see how this statement could help in cutting the triangle in half or in the line and 2 points problem. > The outline of the original (without analytical geometry or
> calculus) proof would be much more interesting. What is wrong with using the most appropriate math tools at hand? Mayas invented zero (independently of Indians) and a very accurate calendar. But surprisingly, they did not even get around to invent a simple division of 2 numbers in artithmetics. Why not ditch this part of arithmetics and do things the Maya's way? > I did not ask for advice on how much time I should spend
> on the problem nor on how to proceed while in the process. Please accept my apology, I mistakenly took the (why??) questions as actual questions, not as challenge questions. Regards, Vladimir |
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|
 |
Vladimir
Member since Jun-22-03
|
Sep-17-03, 08:12 PM (EST) |
    |
9. "RE: Pedal curve of hyperbola"
In response to message #2
| |
LAST EDITED ON Sep-20-03 AT 04:58 PM (EST)
The pedal curve of a given curve with respect to a point P (called the pedal point) is a locus of the heels of normals dropped from P to the tangents of the given curve (see Pedal Curve at MathWorld).The pedal curve of a hyperbola with the pedal point at one focus is a circle centered at the midpoint of the 2 focal points (the intersection of the 2 asymptotes) and with a radius equal to the primary axis of the hyperbola (see Hyperbola Pedal Curve at MathWorld). No proof is given at MathWorld and I found nothing whatsoever on the web. Therefore, I am going to prove it. To simplify things (i.e., to be able to express one branch of the hyperbola as a function y = f(x)), let the primary axis a coincide with the y-axis and the secondary axis b with the x-axis. Equation of a hyperbola with the 2 branches above and below the origin is: y2/a2 - x2/b2 = 1 and the upper/lower branch equations are y = +a/b·Ö(x2 + b2)
y = -a/b·Ö(x2 + b2) Let's put the pedal point into the lower focus - hence the pedal point coordinates are P º {0, -Ö(a2 + b2)} 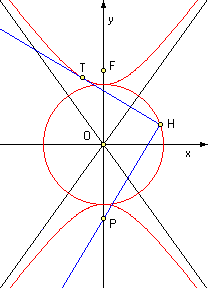
Slope of the tangent to the upper branch of the hyperbola at an arbitrary point xT is a derivative of the upper branch at this point: dy/dx = a/b·xT/Ö(xT2 + b2) and the equation of the tangent is y - yT = a/b·xT/Ö(xT2 + b2)·(x - xT) Since the point of contact T º (xT, yT) is on the upper branch of the hyperbola yT = a/b·Ö(xT2 + b2) y - a/b·Ö(xT2 + b2) = a/b·xT/Ö(xT2 + b2)·(x - xT) Two lines, none parallel to the x and y axes, are perpendicular to each other iff the product of their slopes equals to -1. Hence the equation of the normal to the hyperbola tangent at the point T º (xT, yT) dropped frop the pedal point P º (xP, yP) is y - yP = -b/a·Ö(xT2 + b2)/xT·(x - xP) y + Ö(a2 + b2) = -b/a·Ö(xT2 + b2)/xT·x where I used the coordinates of the pedal point (the lower focus) xP = 0 and yP = -Ö(a2 + b2). To get the equation of the pedal curve, we have to eliminate the coordinate xT of the arbitray point of contact T. Rewriting the equation of the tangent as y - a/b·xT/Ö(xT2 + b2)·x = a/b·Ö(xT2 + b2) - a/b·xT2/Ö(xT2 + b2) and the equation of the normal as x + a/b·xT/Ö(xT2 + b2)·y = -a/b·xT/Ö(xT2 + b2)·Ö(a2 + b2) we can square and add both equations. The whole point of the proof is that now the x·y terms cancel out and the coordinate xT can be factored out: (x2 + y2)·{1 + a2/b2·xT2/(xT2 + b2)} = = a2/b2·(xT2 + b2) - 2a2/b2·xT2 + a2/b2·xT4/(xT2 + b2) + a2/b2·xT2/(xT2 + b2)·(a2 + b2) = = a2/b2/(xT2 + b2)·{(xT2 + b2)2 - 2xT2·(xT2 + b2) + xT4 + xT2·(a2 + b2)} = = a2/b2/(xT2 + b2)·{xT4 + 2xT2b2 + b4 - 2xT4 - 2xT2b2 + xT4 + xT2·(a2 + b2)} = = a2/b2/(xT2 + b2)·{b4 + xT2·(a2 + b2)} = = a2/b2/(xT2 + b2)·{b2·(xT2 + b2) + a2xT2} = = a2·{1 + a2/b2·xT2/(xT2 + b2)} Factoring out {1 + a2/b2·xT2/(xT2 + b2)} eliminates the coordinate xT and yields the equation of the pedal curve: x2 + y2 = a2 which is a circle centered at the origin (the intersection of the hyperbola asymptotes) and with radius equal to the hyperbola primary axis a. Q.E.D. |
Attachments
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f68847d2b0a2102.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f68847d2b0a2102.gif
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|
 |
Vladimir
Member since Jun-22-03
|
Sep-19-03, 05:59 AM (EST) |
    |
10. "RE: Cut triangle in half"
In response to message #2
| |
LAST EDITED ON Nov-02-03 AT 04:19 AM (EST)
Finally, I am in position to perform the construction of cutting the triangle DABC in half by a line l through a given point Q outside the triangle suggested by Golland - using the fact that the cutting line is a tangent to a hyperbola whose asymptotes coincide with the 2 triangle sides intersected by the cutting line and also using the pedal circle of this hyperbola.First, it is necessary to determine, which sides of the DABC will the cutting line l intersect, for there are 3 different hyperbola segments inside the triangle corresponding to 3 different pairs of the triangle sides - the asymptotes of this hyperbola - that the cutting line might intersect. This is done by dividing the plane into 6 sectors by 3 triangle medians. The cutting line will intersect the triangle in the side segment that is in the plane sector containing the given point Q and in the line segment that is in the opposite plane sector. For example, if the point Q is in the plane sector bounded by the medians mb and mc, the cutting line will intersect the side segments CMb and BMc, where Mb and Mc are midpoints of the sides b = CA and c = AB. This was discussed in the original topic #248 - Cut Triangle in Half. 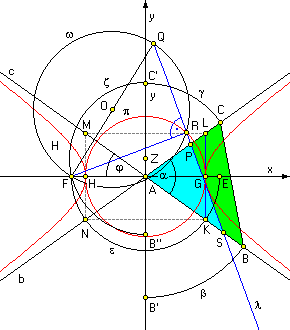
The given point Q in the above drawing is between the medians mb and mc (not drawn). Hence the cutting line will intersect the triangle sides b = CA and c = AB. The extended lines b and c are the asymptotes of our hyperbola. The primary axis of this hyperbola coincides with the bisector of the angle a = Ð CAB, the x-axis in the above drawing, and the secondary axis coincides with a normal to the primary axis erected at the triangle vertex A - the y-axis in the above drawing. Next, we have to find the lengths p and q of the hyperbola primary and secondary axes, respectively (the usual symbols a and b are already reserved for the DABC sides) and the hyperbola focal points E and F. Area of the DABC is S = 1/2·CA·AB·sina = 1/2·b·c·sina Any tangent to the right branch of our hyperbola intersecting the asymptotes b and c at points P and S, respectively, bounds a DASP with an area S/2 S/2 = 1/2·PA·AS·sina = 1/4·b·c·sina
In particular, selecting the tangent perpendicular to the x-axis (the primary axis of the hyperbola) and intersecting the asymptotes b and c in points K and L, respectively, we get an isosceles DAKL, sides of which are equal to the half distance between the focal points r = EF/2 = Ö(p2 + q2) (again, the usual symbol c is already reserved) and altitude AG of which equals to the hyperbola primary axis p. S/2 = 1/2·KA2·sina = 1/2·r2·sina = 1/4·b·c·sina r = Ö(1/2·b·c) To construct the line segment r, transfer the line segments b = AC and c = AB to the y-axis (to the line segments AC' and AB'). Divide one of these line segments in half, say the line segment AB', to get the line segment AB". The length of the line segment B"C' is B"C' = AB" + AC' = c/2 + b. Find the midpoint Z of the line segment B"C' and draw a circle z centered at the midpoint Z and with the radius ZB" = XC' = B"C'/2. The circle intersects the x-axis at points E and F, both at the distance r = Ö(1/2·b·c) from the coordinate origin A. Hence the points E and F are the focal points of our hyperbola (only half of the circle z is drawn). Draw a circle e centered at the coordinate origin A and with the radius r = AE = AF (again, half of the circle e is drawn). The circle intersects the asymptotes b and c at 4 points K, L, M, N forming a rectangle oKLMN, sides of which are KL = MN = 2q and LM = KN = 2p, i.e., double the secondary and primary axes of our hyperbola. The oKLMN intersects the x-axis (the primary axis of the hyperbola) at points G and H, the vertices of the hyperbola. Construct the pedal circle p of our hyperbola corresponding to the pedal point F (the hyperbola focus opposite to the DABC). The pedal circle is centered at the point A (the coordinate origin and the midpoint of the focal points E and F) and it has the radius equal to the hyperbola primary axis p = AG = AH. Find the midpoint O of the line segment FQ, where F is the pedal point focus and Q the given point of the cutting line l. Draw a circle w centered at the midpoint O and with the radius OF = OQ = FQ/2. The circle w intersects the pedal circle p at 2 point, only one of them is labeled as R. Since the lines FR and QR are perpendicular to each other by construction and since the line FR passes through the pedal point, line QR is a tangent to the right branch of the hyperbola and hence the desired cutting line l. The other intersection of the circle w with the pedal circle p would result in a tangent to the left branch of the hyperbola, which does not intersect the triangle DABC and therefore is not a solution of the given problem. This is the most beautiful solution of the problem to cut a triangle in half. However, the construction is not as easy as it'seemed at the first sight - certainly not simpler than the previous constructions solving the appropriate quadratic equations. Moreover, a rather special a priori knowledge is necessary - that all cutting lines are tangents to one of 3 possible hyperbolas and that the pedal curve of a hyperbola with the pedal point in one focus is a circle. Vladimir |
Attachments
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f6aed0b3c1109ae.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f6aed0b3c1109ae.gif
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|
 |
G

guest
|
Oct-15-03, 02:45 PM (EST) |
|
|
11. "RE: Cut triangle in half"
In response to message #10
| |
Hi Vladimir,
It'seems that the topics we so hottly discussed got all tied
together(as they are supposed to on CTK forum!). Let me explain why.
First of all, I want to thank you for bringing up concept of a
polar line. I looked it up on Mathworld. For a conic section: a line thru 2 points A and B on a conic
section is polar line for the point (pole) where two tangent lines
of points A and B cross.
But the most interesting fact on the same page in Mathworld is:
A line thru a pole P point that crosses conic section in points
X and Y and crosses polar line of P in Q has 4 points X,P,Y,Q
tied in a harmonic range, meaning that distances between them are
proportionate to 1,2,3. XP=2,PY=1,YQ=3
This is remarkable, for it allows to do the old construction of
finding 2 points where a transversal crosses ellipse and my
lovely hyperbola. And it also opens some opportunities for the
old circle.
While we know how to draw a tangent to a circle, the ellipse and
hyperbola are more difficult. But using our knowledge from the
now famous on CTK topic ' Cut triangle in half ' we know that
the cutting line is the tangent to hyperbola and the point of
touch is the midpoint between assymptotes. The pedal curve is
the circle touching hyperbola tops.
The pedal curve for an ellipse is its big circle, meaning that any
line tangent to ellipse will reflect from big circle into focus
(see Mathworld).
So construction is clear:
For hyperbola Assume that the point where transversal intersects the small axis
is the pole. Construct the pedal circle and assymptotes.
Using method from the 'Cut the triangle ' draw the tngent line.
midpoint between the assymptotes is the point B.
Draw parallel to main axis thru X till it crosses transversal in Q.
PQ has 4 lengths. Using harmonic range find where points X and Y
are.
For ellipse
Transversal crosses big axis of ellipse in Q. To draw tangents to
ellipse from Q draw a big circle of ellipse and a circle that has
Q and the focus that farther from Q as the diameter. Two circles
cross on tangent line from Q. Draw the polar line.
It crosses our transversal at point P. Using harmonic range numbers
find X and Y.
Nice.
i hope that the number of math errors here (because of my
uncharacteristic excitement) is minimal. Warm regards. G. P.S.
I am asking for an appology of all those who got offended by my
remarks in earlier messages. I put them in lovingly, for I included
myself in the bunch.
|
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|
 |
G

guest
|
Oct-16-03, 05:20 PM (EST) |
|
|
12. "RE%3A Cut triangle in half"
In response to message #11
| |
Hi all, I tried to apply the same harmonic range method to a circle, but
do not see the 2,1,3 intervals there. This made me realize that the construction for ellipse does not
work also, for when transversal thru point P approaches tangent
the intervals change length in opposite direction.
My take from Mathworld was that the harmonic range should apply to
any conic section. What is wrong? Please help. G. |
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|
 |
|
 |
G

guest
|
Oct-16-03, 10:37 PM (EST) |
|
|
14. "RE: RE%3A Cut triangle in half"
In response to message #13
| |
Hi Alex, In Mathworld in section geometry->inversive geometry->polar
they define polar line and pole point for conic sections:
for 2 given points on conic section a line thru them is polar for the
point of intersection of conic section tangents at the given
points. There is a picture of a hyperbola with 2 transversals intersecting
at point Q : one is a polar line thru poits A and B, and the
other one is a line thru pole P and points X and Y on hyperbola. Then they say points X,P,Y,Q form a harmonic range (Wells 1991). The definition of a harmonic range in Mathworld is:
four collinear points A,B,C,D where AB=2,BC=1, CD=3 (see the
picture). Maybe my selection of the pole point on conic section axis is not a
good idea? G. |
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|
 |
alexb
Charter Member
1120 posts |
Oct-16-03, 10:54 PM (EST) |
    |
15. "RE: RE%3A Cut triangle in half"
In response to message #14
| |
Golland, hello: > In Mathworld in section geometry->inversive geometry->polar
> they define polar line and pole point for conic sections:
> for 2 given points on conic section a line thru them is
>polar for the
> point of intersection of conic section tangents at the
>given
> points. Pole/Polar relationship could be defined vertually for any smooth curve. > There is a picture of a hyperbola with 2 transversals
>intersecting
> at point Q : one is a polar line thru poits A and B, and
>the
> other one is a line thru pole P and points X and Y on
>hyperbola.
>
> Then they say points X,P,Y,Q form a harmonic range (Wells
>1991). Right. But the four points in this case are collinear. > The definition of a harmonic range in Mathworld is:
> four collinear points A,B,C,D where AB=2,BC=1, CD=3 (see
>the
> picture). This is something very special. I do not know what he uses it for. > Maybe my selection of the pole point on
> conic section axis is not a good idea? Can't say. What I do know is that cross-ratio, which is this double ratio AC/AD : BC/BD, for collinear points is a projective invariant. The harmonic ratio is defined by the same experession where A, B, C, D are complex numbers. This is Moebius function invariant even if the numbers are not collinear. (AB = B - A.) If A, B, C, D are treated as points in the plane, then the double ratio is invariant under inversion. So it looks like you always get either straight lines or circles, not more general conics. |
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|

You may be curious to have a look at the old CTK Exchange archive.
Please do not post there.

|Front page|
|Contents|
Copyright © 1996-2018 Alexander Bogomolny
73596047
|
|
|