LAST EDITED ON Aug-11-03 AT 01:24 AM (EST)
You have a DABC in its circumcircle. Add any 4th point D on the circumcircle and you have a cyclic quadrilateral ABCD. You want to construct point D (on the selected arch BC) such that the cyclic quadrilateral ABCD also has the incircle.Once you see the solution, it is rather simple. Please note that I am constructing the point D on the arch AC (not BC) and that the angle ABC = b > 90°. Minor differences would be necessary for b < 90°.
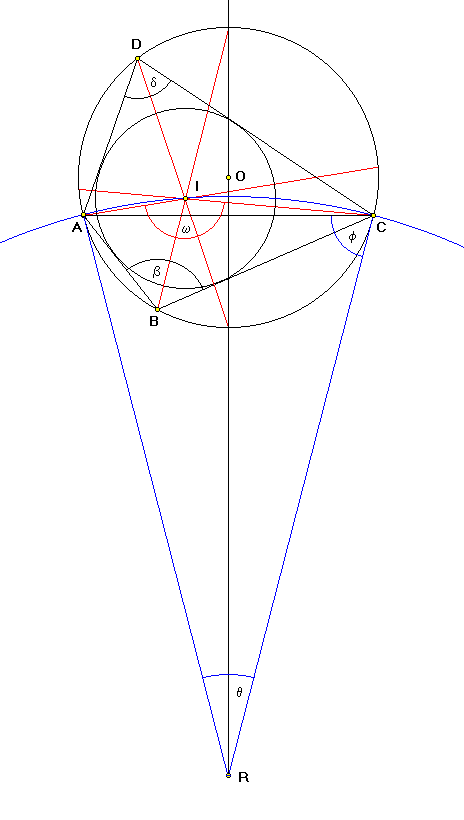
1. Angles a, b, g, and d are angles at vertices A, B, C, and D, respectively (only b and d are marked in the above drawing). The incenter I is on bisectors of all 4 inner angles a, b, g, and d of the quadrilateral ABCD. We can construct the bisector of the angle b.
2. The quadrilateral ABCD is cyclic. Therefore opposite angles add up to 180°.
a + g = 180°
b + d = 180°
Since the rays AI and CI are bisectors of the angles a and g, angle AIC = w equals to
w = 360° - (a + g)/2 - b = 270° - b
The incenter I is on an arch defined by the points A and C and by the angle w. To find the center R and radius AR = CR of this circle, construct an isoscleles DACR opposite to the arch AC, such that the side AR = CR and the angle ARC = q equals to
q = 360° - 2w = 360° - 2·(270° - b) = 2b - 180°
The remaining 2 angles ACR = CAR = f of the isoscleles DACR (those we are going to construct) equal to
f = {180° - (2b - 180°)} / 2 = 180° - b
3. The circle with the center R and radius AR = CR intersects the bisector of the angle b at the point I, the incenter of quadrilateral ABCD. Once we have the incenter I, we can find the point D by doubling the angle BAI = a/2 or the angle BCI = g/2 or both. The rays AD and CD intersect at the point D on the circumcircle of the DABC.
Printer-friendly copy
Email this topic to a friend
