Ever since I learned about the Steiner's theorem, the weakness of my constructions using the compass once or the square once was clear to me. They are constructions for basic steps such as drop a normal or draw a parallel. A complex geometrical construction takes many basic steps and if I choose the single circle center and/or radius or the single square center, half-diagonal, and/or orientation for one basic step, I will not be able to choose them for the next basic step. I never saw these construction as anything but stepping stones in the process of finding and learning the basic construction where the circle or square are given, period. Because only in this way I can proceed in a complex geometrical construction. I could not find these basic constructions in the library and I could not find them on the web.

Now, beside the geometrical constructions with one circle or one square given, period, there are (beautiful) geometrical construction in which we use the compass liberaly, selecting the center and/or radius every time. It'seems to follow from the Steiner's theorem, that the constructions using the compas liberaly can be all performed using the square liberaly, constructions I did not know about, probably no less beautiful than the compass constructions. In order to think about or try such construction, it is necessary to know what limitations should be observed in placing the square. It does not matter that there is no square drawing tool, I can always draw a square somehow and pretend that it has been drawn by the tool. Just like we draw parallels by shifting triangle shaped rulers, because we know that we could construct them if necessary. It does not take away the beauty of the construction. I am almost sure that choosing the square center and/or half-diagonal should be allowed (in constructions using the square liberaly!!!), but I am still uncertain about choosing the square orientation - I will have to think about it. I do not see any reason for disagreement.

Regards, Vladimir

Given a circle w with the center O and a line k º AB passing through the circle center, we can draw a parallel l to this line through and arbitrary point D on the circle using the basic straightedge construction #1 (see Drop a normal) with the line seqment AB and its midpoint O. Since the new line l does not pass through the circle center, we can erect a normal to this line at either of its 2 intersection points C, D with the circle w using a straightedge alone. Subsequently, we can shift this normal to any point on the line k º AB using the basic straightedge construction #1 with the line segment DE and its midpoint F.

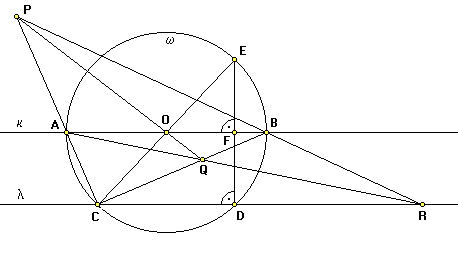
Given a circle w with the center O and a line k º AB intersecting the circle but not passing through the circle center, we can erect a normal to this line at either point of intersection A or B and complete the rectangle ABCD using a straightedge alone. Then we draw a parallel to the rectangle diagonal AC through an arbitrary point A' on the circle w using the basic straightedge construction #1 with the line seqment AC and its midpoint O. Once we have the parallel A'B', we can complete another rectangle A'B'C'D' using a straightedge alone. Subsequently, we can shift this normal to any point on the line k º AB using the basic straightedge construction #1 with the line segment EF and its midpoint C.

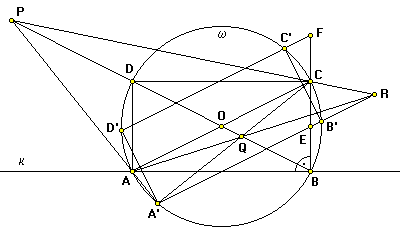
Conversly, given a circle w with an unknown center, if we can erect normals to any 2 lines k, l intersecting the circle at their intersection points with the circle, we can complete the construction of the circle center O with a straightedge alone.

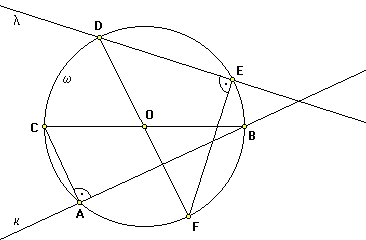
Hence, the ability to erect a normal to a line intersecting the circle with a straightedge alone is equivalent to having the circle center.

Suppose it is possible to erect a normal to a given line with a straightedge alone and without having the center of any circle at our disposal. Since lines project to lines under the parallel projection, any parallel projection of such a construction follows the same rules as the actual construction and must also yield a normal, which is of course absurd. Therefore, it is not possible to find a circle center with a straigtedge alone.