Here is a problem involving geometry and trig.

Given a billiard table in the form of a right triangle ABC with B the right angle. Let the cue ball be struck at vertex A and bounce off sides BC, AC, AB, and AC finally arriving at vertex B. The angle of reflection equals the angle of incidence at each bounce. The points of bounce are D, E, F, and G respectively. If the path segments AD, EF, and GB are concurrent, then what is the value of

75 * { tan(<BAC)^2 - tan(<BAD)^2 }

Bractals

maybe I did it differently to you... did you use a lattice at any point?
(oh, and 16)

Thankyou

sfwc
<><

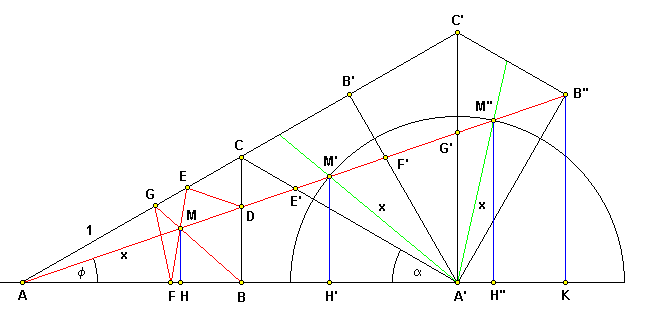
Let's denote the table angle BAC as a and the initial ball angle BAD as f and let's select the table hypotenuse AC as the unit length. Coordinates of the endpoint B" of the straightened ball path ADE'F'G'B" are

B" º { cosa (2 cosa - cosa cos4a), cosa sin4a }

Tangent of the ball angle f is then

tanf = sin4a / (2 - cos4a)

Note that if p/2 < 4a < p (as in the above drawing), then 0 < p - 4a < p/2

sin(p - 4a) > 0
cos(p - 4a) > 0

sin(p - 4a) = sinp cos4a - cosp sin4a = sin4a
cos(p - 4a) = cosp cos4a + sinp sin4a = -cos4a

The upper limit for the billiard table angle a is

sin4a > 0
4a < p
a < p/4 (45°)

The lower limit is given by the expression

tana > sin4a / (2 - cos4a)
a > ~24.7°

If the table angle is out of these limits, the ball can never reach the point B, not to mention any path concurrence.

Since the ball paths AD, EF, and GB are concurrent - they intersect at the point M, the images M' and M" of this point are on the line AB" and at distance x = AM = A'M' = A'M" from the point A'. Coordinates of the points M' and M" are

M' º { 2 cosa - x cos(2a - f), x sin(2a - f) }
M" º { 2 cosa - x cos(4a - f), x sin(4a - f) }

As the right angle trianlges DABD, DAHM, DAH'M', and DAH"M" are all similar, we have

tanf = x sin(2a - f) / (2 cosa - x cos(2a - f))
tanf = x sin(4a - f) / (2 cosa - x cos(4a - f))

Solving both equations for x

x = 2 cosa tanf / (sin(2a - f) + tanf cos(2a - f))
x = 2 cosa tanf / (sin(4a - f) + tanf cos(4a - f))

x = 2 cosa sinf / (cosf sin(2a - f) + sinf cos(2a - f))
x = 2 cosa sinf / (cosf sin(4a - f) + sinf cos(4a - f))

x = 2 cosa sinf / sin2a
x = 2 cosa sinf / sin4a

Combining the 2 equations

2 cosa sinf / sin2a = 2 cosa sinf / sin4a
sin4a = sin2a

Within the limits for the table angle 24.7° < a < 45° (even within wider and simpler limits 0° < a < 45°), this is only possible if

4a = p - 2a
a = p/6 (30°)

Using the tangent of the initial ball angle f deduced from the coordinates of the path endpoint B"

4a = 2p/3
tanf = sin4a / (2 - cos4a) = sin(2p/3)/(2 - cos(2p/3)) = (Ö3/2) / (2 + 1/2) = Ö3/5
f ~ 19.1°

I have no idea why the following expression has any importance, did not have to use a single square in the solution.

75 (tan²a - tan²f) = 75 ((Ö3/3)² - (Ö3/5)²) = 75 (1/3 - 3/25) = 25 - 9 = 16