|
|

|
|Store|
|

|

|

|
|

|

|

|

CTK Exchange
Kevin Fite

guest
|
Oct-18-03, 11:43 AM (EST) |
|
|
"Great Middle School Word Problem"
| |
Mr. Howard asked 100 of his students who could play chess. Half of the boys said yes and two-thirds of the girls said yes. 17 of the boys said no. How many total students can play chess? Scroll down for the answer Kevin Fite
www.mathbeyondtherealm.com
Detroit,MI The answer is 61 because 17 boy said no which means 17 boys said yes because half the boys said yes. Since there are 34 boys, it has to be 66 girls and 2/3 of 66 is 44. And 44 + 17 is 61. Enjoy
|
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
Vladimir
Member since Jun-22-03
|
Oct-22-03, 00:00 AM (EST) |
    |
1. "RE: Great Middle School Problem"
In response to message #0
| |
Nice little problem, even though the conditions are unrealistic. I used to play in low level chess tournaments and girls were very few, perhaps 1:100 or less. Still, we all admired those few who also loved the game. I came across this nice little problem in San Francisco Bay Area Math Bowl competition: Find the area of a trapezoid with sides of length 2, 3, 3 and 6, where the sides of length 3 and 6 are parallel. The answer is given as 4·Ö5, but I cannot get it - I am getting 6·Ö2. Might there be a typo? I tried to change the trapezoid sides to length of 4, 3, 3, and 6, sides of length 3 and 6 being parallel (3, 3, 3 and 6 would be trivial). This is a little bit harder, but then I get the area 6·Ö5 (2 typos?). Or suppose the trapezoid has the sides of length 2, 3, 3 and 5, sides of length 3 and 5 being parallel. This is still a notch harder and I get the area as 3·Ö7. Would anybody care to try? Regards, Vladimir |
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
 |
|
 |
|
 |
Brian Steuer

guest
|
Nov-01-03, 01:50 AM (EST) |
|
|
3. "RE: Great Middle School Problem"
In response to message #1
| |
I also get 6 * 2^.5: The trapezoid can be broken into a rectangle of width 3 and height a, a triangle of hypotenuse 2, height a, and width b, and a triangle of hypotenuse 3, height a, and width c. a^2 + b^2 = 2^2 a^2 + c^2 = 3^2 So, c^2 - b^2 = 3^2 - 2^2 = 5 Also, b + c + 3 = 6, so b + c = 3 c^2 - b^2 = (c - b) * (c + b) = (c - b) * 3 So, 3 * (c - b) = 5, c - b = 5/3 c + b = 3 2c = 3 + 5/3 c = 7/3 b = 2/3 a^2 + (2/3)^2 = 4 a^2 = 32/9, a = 4/3 * 2^.5 The area of the rectangle = 3 * a = 4 * 2^.5 The area of One triangle = .5 * a * b = 4/9 * 2^.5 The area of the other triangle = .5 * a * c = 14/3 * 2^.5 So, the area of the entire trapezoid = (4 + 4/9 + 14/9) * 2^.5 = 6 * 2^.5 |
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|
 |
Vladimir
Member since Jun-22-03
|
Nov-02-03, 12:13 PM (EST) |
    |
4. "RE: Great Middle School Problem"
In response to message #3
| |
LAST EDITED ON Nov-04-03 AT 05:13 PM (EST)
Hello Brian,Thank you, I am glad we are in agreement. (You have a typo in the last but one line, which you can always fix by editing your message, but the last line is correct). A sketch always helps: 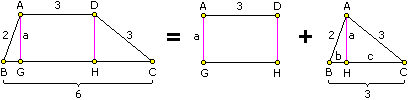
Of course, you can calculate the area of a trapezoid with the sides of length 4, 3, 3, 6, sides of length 3 and 6 being parallel, in exactly the same way, it is not harder at all - I was wrong in this detail. But there is a little catch if the sides are of length 2, 3, 3, 5, sides of length 3 and 5 being parallel. Possibly the simplest construction of the trapezoid ABCD (AB = 2, BC = 6, CD = 3, AD = 3, BC || AD) is as follows: 1. Draw a line segment BC of the length 6 units. 2. Draw 2 circles b and g centered at the points B and C and with radii 2 and 3 units, respectively. 3. Translate the circle b by AD = 3 units right (AD being the shorter parallel side of the trapezoid) into the circle b' centered at the point B' (such that BB' = AD = 3 and B' is on the line BC). The translated circle b' intersects the circle g at the point D. 4. Draw a parallel to the line BC through the point D. The parallel intersects the circle b at the point A. 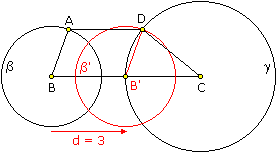
Regards, Vladimir
|
Attachments
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3fa4caad78374239.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3fa4caad78374239.gif
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3fa4d84907378493.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3fa4d84907378493.gif
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|
 |
|
 |
paul

guest
|
Nov-13-03, 08:42 PM (EST) |
|
|
7. "RE: Great Middle School Problem"
In response to message #1
| |
no the answer is 4*root of 5...
u know the the sloping opposite sides are length 3.
breaking the trapeziod into a rectangle and 2 triangles, u can see that the base of each triangle is 2.
using pythagorean theorem to find the distance between the 2 parallel sides...
hypotenuse^2 = height^2 + base^2
3^2 = height^2 + 2^2
9 = height^2 + 4
thus,
height = root of (9-4)
= root 5.area of rectangle = base x height
= 2 x root 5. area of triangle = 1/2 x base x height
= 1/2 x 2 x root 5
= root 5 total area = triangle area + other triangle's area + rectangle's area
= root 5 + root 5 + 2 x root 5
= 2x root 5 + 2x root 5
= 4 x root 5.
:) |
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|
 |
Vladimir
Member since Jun-22-03
|
Nov-14-03, 07:47 AM (EST) |
    |
8. "RE: Great Middle School Problem"
In response to message #7
| |
LAST EDITED ON Nov-23-03 AT 11:11 AM (EST)
Hello Amit and Paul,The problem in San Francisco Bay Area Math Bowl competition is stated as follows: Find the area of a trapezoid with the sides of length 2, 3, 3, and 6, where the sides of length 3 and 6 are parallel. The given (and incorrect) solution is 4Ö5. The correct solution is 6Ö2, as Brian calculated above. You are both solving a slightly different problem: Find the area of a trapezoid with the sides of length 3, 2, 3, and 6, where the sides of length 2 and 6 are parallel. 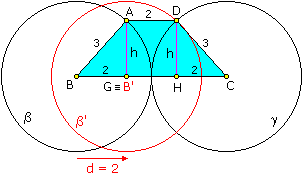
This makes the trapezoid isosceles, which simplifies the solution. The height of the trapezoid is now h = AG = Ö(AB2 - BG2) or h = DH = Ö(CD2 - CH2) Since the trapezoid is now isosceles, BG = CH = (BC - AD)/2 = (6 - 2)/2 = 2 and the height is h = Ö(32 - 22) = Ö5 The area then really is A = (BC + AD)/2 · h = (6 + 2)/2 · Ö5 = 4Ö5 but it is solution of a different problem. Indeed, this probably identifies the typos in the original problem as given in the San Francisco Bay Area Math Bowl competition.
__________________________________________________________________
Now, suppose that we have to find the area of a trapezoid with the sides of length 2, 3, 3, and 5, where the sides of length 3 and 5 are parallel. The little catch is that now the trapezoid has an obtuse angle at its longer base: 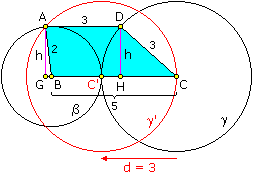
but the solution presented by Brian still works. Height of the trapezoid is h = AG = Ö(AB2 - BG2) and also h = DH = Ö(CD2 - CH2) Hence AB2 - BG2 = CD2 - CH2
CH2 - BG2 = CD2 - AB2 = 32 - 22 = 9 - 4 = 5 On the other hand, CH - BG = BC - AD = 5 - 3 = 2 We have CH2 - BG2 = (CH + BG)·(CH - BG) = 5
CH - BG = 2 Therefore CH + BG = 5/2
CH - BG = 2 Solving for CH and BG by adding and subtracting the 2 equations: 2·CH = 5/2 + 2 = 9/2
2·BG = 5/2 - 2 = 1/2 CH = 9/4
BG = 1/4 Calculating the trapezoid height: h = Ö(AB2 - BG2) = Ö(22 - (1/4)2) = Ö(4 - 1/16) = Ö{(64 - 1)/16} = Ö(63/16) = 3/4·Ö7 Check by calculating the trapezoid height from the other equation for h: h = Ö(CD2 - CH2) = Ö(32 - (9/4)2) = Ö(9 - 81/16) = Ö{(144 - 81)/16} = Ö(63/16) = 3/4·Ö7 as required. The area of the trapezoid is then A = (BC + AD)/2 · h = (5 + 3)/2 · 3/4·Ö7 = 3Ö7
__________________________________________________________________ Thank you all. Regards, Vladimir
|
Attachments
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3fb474be18be322d.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3fb474be18be322d.gif
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3fb4792120199199.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3fb4792120199199.gif
|
|
Alert | IP |
Printer-friendly page | Edit |
Reply |
Reply With Quote | Top |
|
|
|

You may be curious to have a look at the old CTK Exchange archive.
Please do not post there.

|Front page|
|Contents|
Copyright © 1996-2018 Alexander Bogomolny
73601116
|
|
|