![]()
Problem
In my business we occasionally need to cut across large diameter plastic or steel pipe at a 45 degree angle. By wrapping a piece of thin carboard around a cut pipe I can make a template which, when layed flat, looks like a bell curve. Can you provide me with the general mathematical formula that defines this curve for any diameter pipe that we might have to cut?
![]()
Solution
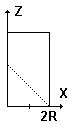
Let's position the pipe in such a way as to have Z axis run along one of its generating straight lines, X axis pass through the center of its cross-section and Y axis tangent to the pipe (in the diagram on the left Y axis points away from the screen.) Assume also that the plane of the supposed cut is described by X+Z=2R where R is the radius of the pipe.
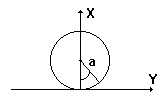
The top view is present in the diagram on the right. Let the central angle a be 0 at the bottom of the circle. The positive direction is taken counterclockwise, as usual. Then X=R-Rcos(a).
We want to express Z in terms of L - the arc length of the circumference. We can imagine unfolding of the latter to coincide with a segment of Y axis after being cut at the top point (2R, 0). Accordingly, let L change from 0 for a=-π to 2Rπ for a=π. This gives L(a)=Ra+Rπ. In other words a=L/R-π.
From here and X+Z=2R we get
![]()
73581482
