|
Starting with S(1) = 1, S(2) = 36, and so on. Proof is fairly
straightforward. Well, it seems curious that a thing can be both a
triangle and a square, doesn't it?
Yes, of course. How can something be square and triangular simultaneously?
Well, I had to look through several books in my library till I discovered a discussion of these numbers in A. H. Beiler's Recreations in the Theory of Numbers. Beiler writes: "Eight triangles increased by unity produce a square," because
| (2) |
8·r(r + 1)/2 + 1 = 4r2 + 4r + 1 = (2r + 1)2.
|
(2) proves the converse as well: a square decreased by unity gives eight triangles.
This simple rule explains the recurrence relation (1). However, (1) does not enumerate all such numbers. From (1), we get S(3) = 41616, whereas there is another number, 1225, that is both triangular and square: 1225 = 49·50/2 = 352.
The question was in fact posted as the problem E1473 (AMM, 1962, p. 168) by J.L. Pietepol and solved by A.V. Sylvester [Mathematical Morsels, p. 145, Mathematical Quickies, #186]. Let Tn = n(n + 1)/2 denote the nth triangular number. The solution follows from the observation that if Tn is a perfect square, so is T4n(n+1). Indeed, let n(n + 1)/2 = k2. Then 4n(n + 1) = 8k2. Continue:
| |
| T4n(n+1) = T8k2 |
= 8k2(8k2 + 1)/2 = 4k2(8k2 + 1) |
| = 4k2[4n(n + 1) + 1] = 4k2[4n2 + 4n + 1] |
| = 4k2(2n + 1)2. |
|
All such numbers can be found by solving a Pell equation: 8x2 + 1 = y2 which plays a prominent role in number theory.
| Numbers Simultaneously Square and Triangular |
|---|
| 8x2 + 1 = | y2 | Triangular number | Side of triangle | Side of square |
|---|
| 8·12+1 = | 32 | 1 | 1 | 1 |
| 8·62+1 = | 172 | 36 | 8 | 6 |
| 8·352+1 = | 992 | 1225 | 49 | 35 |
| 8·2042+1 = | 5772 | 41616 | 288 | 204 |
| 8·11892+1 = | 33632 | 1413721 | 1681 | 1189 |
| 8·69302+1 = | 196012 | 48024900 | 9800 | 6930 |
| 8·403912+1 = | 1142432 | 1631432881 | 57121 | 40391 |
All such numbers can be obtained by squaring the members of the sequence generated from the recurrence relation
| (3) |
un = 6un-1 - un-2, n > 1, u0 = 0, u1 = 1,
|
There is also an explicit formula
| (4) |
un = (((1 + √2)2n - (1 - √2)2n)/(4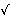 2))2 2))2
|
which can also be written as [Wells, p. 93]
| (4) |
un = [(17 + 12√2)n + (17 - 12√2)n - 2]/32.
|
([Wells, p. 93] also mentions that no triangular number may be a cube, or fourth or fifth power.)
Armando Guarnaschelli from Argentina found a very simple recurrence relation that generates all triangular numbers that are also square.
References I came across are listed below.
References
- A. H. Beiler's Recreations in the Theory of Numbers, Dover, 1966
- J. H. Conway, R. K. Guy, The Book of Numbers, Springer, 1996
- R. Honsberger's Mathematical Morsels, MAA, 1978
- G. M. Phillips, Mathematics Is Not a Spectator Sport, Springer, 2005
- C. W. Trigg, Mathematical Quickies, Dover, 1985
- D. Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Books, 1987

|Contact|
|Front page|
|Contents|
|Did you know?|
Copyright © 1996-2018 Alexander Bogomolny
73371974
|
