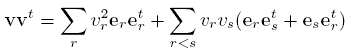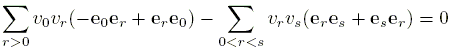Clifford Algebras and Vector Fields

By Hubert Shutrick
May 17, 2009

Clifford Algebras

In the article on the shaggy dog theorem, it was stated that vector felds on spheres can be constructed using Clifford algebras. Here, the attempt is to give some idea of how this is done assuming only a knowledge of basic linear algebra.

An algebra over the real numbers R is a real vector space with a multiplication (u, v) → uv that is associative and bilinear, that is,

An example is the algebra R(n) of n×n real matrices considered as an n² dimensional vector space with the usual matrix product. Bold face symbols will denote vectors and matrices.

The Clifford algebra C_k is the algebra over the reals with unit element e₀ so

and multiplicative generators e₁, e₂, ..., e_k that satisfy

for all r, s = 1, 2, ..., k.

The second relation implies that any product of the generators can be reordered so that the suffces are in ascending order and then duplicates can be eliminated using the first relation. Therefore, there is an additive basis that consists of e₀ and products of the generators one for each non-empty subset of the numbers 1, 2, ..., k, the product whose suffces in ascending order. The algebra has dimension 2^k.

C1	has basis e0, e1 with the single relation e1² = - e0. It is, of course, the complex numbers C with e0 = 1 and e1 = i, where 1 is the identity matrix in R(2) and i is the matrix   0 - 1 1 0 because multiplying the column vector (x, y) by it gives (-y, x).
C2	is the quaternions H with e0 = 1 = the identity in R(4),   e1 = i = 0 - 1 0 0 1 0 0 0 0 0 0 - 1 0 0 1 0 , e2 = j = 0 - 1 0 0 1 0 0 0 0 0 0 - 1 0 0 1 0 This can be verifed by checking the relations.
C3	turns out to be the tensor sum H⊕H, which can be considered as the algebra of 2×2 diagonal matrices with entries from the quaternions or block matrices in R(8). Thus, e0 is the unit matrix and a set of generators is   e1 = i 0 0 - i , e2 = j 0 0 - j , e3 = ij 0 0 - ij
C4	is the algebra H(2) of all 2×2 matrices and a set of generators is the same as for C3 with the addition of   e4 = 0 1 -1 0

There is, of course, a smart way of calculating the Clifford algebras to be found in the literature. It gives, with the same convention for the matrix algebras,

and after that there is an eight-fold periodicity because C_{k + 8} is the matrix algebra C_k(16).

For instance, the algebra C₁₀ will be H(16), a subalgebra of R(64).

Vector Fields on Spheres

The sphere S ^n-1 is the set of unit vectors in Rⁿ and a tangent vector at u is a vector v that is orthogonal to it. A tangent vector field is a continuous mapping from the sphere such that u maps to a non-zero tangent vector at u. If the sphere has k independent tangent vector fields they can be made orthonormal at each point using one of the standard methods.

The first example is the circle S ¹ with the unit tangent vector pointing anticlockwise. If the circle is regarded as the set of complex numbers of unit norm, then the field is given by z → iz. Moreover, if S ^2n-1 is considered as the unit sphere in Cⁿ then

is a tangent vector field. Every odd dimensional sphere has then at least one tangent vector field. The same works with the quaternions. H = R⁴ and we consider 1, i, j, ij as an orthonormal basis. If (a, b, c, d) is a point in S ³, that is, a unit vector in R⁴, then multiplying by i gives

so (a, b, c, d) becomes (-b, a, -d, c), which is an orthogonal unit vector, a tangent vector at the point. Multiplying by j and by ij give two more tangent vectors at the point and a calculation shows that the three are orthonormal. There are then three independent tangent vector fields on the three sphere. This can also be extended to show that S ^4n-1 has at least three independent tangent vector fields.

Theorem. If the generators of C_k act linearly on Rⁿ, then S ^n-1 has k independent vector fields. The n×n matrices that give the action of the generators will be orthogonal if the scalar product on Rⁿ is suitably chosen. This is because the additive basis elements of Ck along with their negatives form a group G of order 2^k+1 under multiplication. In that case, the new scalar product obtained from the standard one u·v by

(where the summation is over all g ∈ G) is such that (gu|gv) = (u|v) for all g ∈ G because multiplying by g just permutes the elements of the group. Since the action of the generators preserves this scalar product, it is orthogonal with respect to a new orthonormal basis.

Consider the (k + 1)-dimensional real vector space V with orthonormal basis e₀, e₁, ..., e_k from C_k. It acts linearly on Rⁿ by linearly extending the action of the generators and e₀, which acts as the identity matrix. The action gives a bilinear mapping V×Rⁿ → Rⁿ. The theorem will be proved if we can show that, for each point u in S ^n-1 ⊂ Rⁿ the mapping from V to Rⁿ given by acting on u preserves scalar product because the images of the generators will then be an orthonormal set of tangent vectors. Preserving scalar product is equivalent to preserving norm since

and it is suffcient to show that it takes unit vectors to unit vectors, which will be true if the matrices of unit vectors v in V are orthogonal. The condition that v is orthogonal is that its transpose v^t is its inverse:

The generators and e0 are orthogonal so the first sum is e₀. The inverse of each generator is its negative so the second sum becomes

As an example, note that C₇ = R(8)·R(8) and it acts on R⁸ by the action of the first factor in the tensor sum and so the sphere S ⁷ has seven independent vector fields. The three on S ³ were given by the action of H but this is the same as the action of C₇ by the first factor in the vector sum so it agrees with the theorem.

As a final example that illustrates the general formula below, consider C₁₁ = C₃(16). It can be converted into the block matrix form H(16)⊕H(16) by rearranging the rows and columns. It acts through the first factor on H¹⁶ = R⁶⁴ giving 11 independent tangent vector fields on S ⁶³.

The formula for the number of independent vector fields on S ⁿ is, if n + 1 is divisible by 16^a but not 16^a+1 and if the quotient is divisible by 2^b, then there are 2^b + 8a - 1 of them. They can all be obtained in this way and Adams proved that there are not more of them.

References

1. J. F. Adams, Vector Fields on Spheres, Bull. Am. Math. Soc., 68: 30-41 (1962)
2. J. F. Adams, Vector Fields on Spheres, Bull. Am. Math. Soc., 75: 603-632 (1962)
3. D. Husemoller, Fibre Bundles, McGraw-Hill Book Company, New York, 1966