 |
Cut The Knot!by Alex Bogomolny |
Chance Encounters at ICME-9
September 2000
Many of my impressions from ICME-9 came from personal, often unplanned, meetings. After a lecture by N. P. Dolbilin Geometry in Russian Schools, I ran across N. N. Konstantinov - a well known mathematics teacher in the Moscow math circles. In 1960s, Moscow saw a crop of a new kind of schools - special schools that emphasized instruction in a specific subject. Konstantinov was among the organizers of the special math school #57. His first question to me (in my literal translation) was, "What school are you from?" My reply, "The Moscow State", was met with protests. "No, no. What I mean is what school are you from?" I chuckled. Do we still talk schools at the distance of some 30+ years? "Well, it was the #444." "Ah", he appeared quite satisfied, "Shwartzburd!" - referring to the founder of my school - "That's good." I felt privileged and enchanted.
In the lecture Dolbilin outlined the history and the current state of geometry education in Russia. Up to the late 1970s, all schools across Russia shared the same geometry curriculum and the same textbook. The book, by A.P. Kyselev, was first published in the 1890s. Kyselev was an outstanding pedagogue which may explain the longevity of his book. There might be another reason though. Dolbilin expressed what I believe to be a commonly held view in Russia. He said, "A good teacher does well with any textbook." A similar opinion is being entertained with respect to bad teachers.
After a short-lived (New Math) reform that bolstered an increase in textbook production, the tradition has been re-established. Two modern texts have been written and kept in service with no competition for about 20 years. The situation began changing due to the Perestroika that had a profound effect on all aspects of life and education in Russia. In the spirit of free enterprise, Konstantinov teamed up with several world renowned mathematicians (V.I. Arnold, S.P. Novikov, Ya.G. Sinai, A.A. Kirillov) to found the Independent University of Moscow - a private institution whose express goal is to train professional mathematicians. (Truth be told, students do take classes in French in addition to the mathematics.) The textbook market also became more competitive. Dolbilin specifically pointed to books (rigorous and intuitive at the same time) by Igor Sharygin(*).
I had met Sharygin the day before. He was busily talking to several people at the same time, but somehow managed to press into my hands a Samizdat (self-published) brochure Two Articles and Two Hundred Problems. For whatever reason, he opened the brochure on the last page and pointed to the last problem - "This is a good one." When, after Dolbilin's lecture, I wanted to tell him my solution he interrupted me with a smile, "It's all such-and-such numbers, right?" I had only to nod in agreement. (Can't tell you just now what numbers they were; for this would give away the solution.)
The first article in the brochure - Mathematical Education and Society (an outlook from Russia and into Russia) - was an outpouring of concern from an insider who is painfully aware of the decline of mathematics education in Russia. Besides many reasons common to other countries, the deteriorating economic situation has negatively affected the whole of education system in Russia. Perestroika turned out to be a two-faced Janus. According to Sharygin, one of the current ills of mathematical education in Russia is its "Americanization", pragmatism in education being one of the manifestations. He writes
... pragmatism is especially profitable when you live among idealists. Society consisting exclusively of pragmatists is lacking vitality as well as society including just idealists.
This consideration applies to all countries, the US in particular. However,
The American science is supported by "the world brain" contrary to the Russian science which is sustained by its own brains. The decline in mathematical education may destroy the Russian science once and for all.
And also
The Paradox is that American mathematical education itself is one of the worst in the world, but the system of American mathematical education as a whole is probably the best, since the whole world is integrated into it.
While I agree with much of Sharygin's argument and empathize with the rest, I believe that the idea that "the whole world is integrated" into the American mathematical education system is an exagerated remnant of the cold war upbringing, when the whole world was divided into two categories of them and us. Now that the USSR ceased to exist and Russia does not quite measure up to the status of a superpower, it may be natural to think of the American education in global terms. There is little doubt however that, for example, French, Chinese or Japanese education systems have been evolving very much on their own. This of course did not protect them from developing home grown shortcomings. None is perfect.
Can College Mathematics in Japan Survive? was a dramatic title of a talk presented by Yukihiko Namikawa from Nagoya University. It appears that the problem faced by Japanese colleges is twofold. On one hand, the child population in Japan dwindles steadily. One projection has it that by the year 2009 population of potential students will be so low that colleges will have to admit all applicants in order to fill their teaching capacity. On the other hand, declining ability and knowledge of college freshmen has been observed yet in early 1990s. In 1994, the Mathematical Society of Japan established a working group to study the brewing crisis. For an outsider, these facts may come as a great surprise. Indeed the results of the Third International Mathematics and Science Study (TIMSS) suggest a more positive picture of the Japanese education. TIMSS has been conducted during the 1995 school year in three age groups: 4th grade, 8th grade, and the last year of the secondary school. True, Japan only participated in the first two, but in both she was placed third after Singapore and Korea and far ahead of the USA. Do not you see inconsistency in Japanese students' performance across the grades?
Yoshihiko Hashimoto (Yokohama National University) whom I met one day at breakfast did not. To explain the situation he drew a diagram on a napkin:
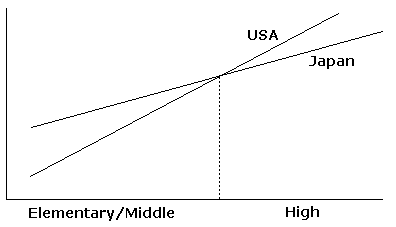
Which is a fine example of how mathematics helps find patterns in real life. This is also an example where it did not help to see the invisible. The reasons for the above statistics remained unclear. One plausible explanation that we talked about was family participation. Almost every parent is able to oversee child's performance in early grades and help when necessary. As the child advances through the grades, fewer parents have adequate knowledge to lend a helping hand. Now, Professor Hashimoto gave an interesting talk in April at the NCTM Annual Conference in Chicago. There he quoted statistics according to which Japanese middleschoolers know mathematics better than their American counterparts but like it less. That morning in Makuhari it crossed my mind that parents who lost the ability to help their child could try to compensate by enforcing a more rigid schedule and discipline which might lead the child to dislike the subject.
Of course it's futile to speculate about the culture one knows so little about. I did try to keep my eyes open, but 10 days I spent there were too little of an opportunity to get a real feeling for things Japanese. I left Japan with a notion that, if anything, it's more like Iowa than New York. Here's how I got that idea.
One evening on the way to my hotel I was stopped by an elderly person who introduced himself as a vegetarian in search of a fresh fruit market. He turned out to be a retired school principal from Israel. Chaim Orbakh was his name and at the Congress he was representing his company - Or International. Once between the lectures I went looking for him in the exhibition hall. He had a table and a chair by one of the walls. Prominent among his offerings was the Verifier - a small gadget that consists of a transparent plastic box with a removable top and a bottom with 2x6 markings to accommodate 12 square counters. On one side of the counters there are numbers from 1 through 12. The back sides form a pattern:

The gadget comes with a number of booklets, each offering a few dozens exercises. An exercise consists of 12 problems and a pattern. The problems are arranged in a 2x6 matrix the size of the gadget. Place the gadget on top of the exercise and match counters with answers to the problems. After all problems are answered, close the gadget and turn it around. Verify that the answers are correct by comparing two patterns: the given one and the one on the back side of the gadget. The booklets offer a variety of pattern matching and arithmetic exercises covering grades K-6.
Here's a Java simulation for arithmetic problems. (The gadget with the problems is located in the lower portion of the applet. The "answer" tiles form the upper two rows. Click on an answer first, then on the problem. To remove a solution click first on a problem and then on an empty tile space. )
(Now let's think about it. A set of exercises with a predefined set of solutions serves as its own verifier. To make it work smoothly start with the more difficult exercises and move towards the easier ones. If at some point you can't find a solution to match a problem, a mismatch must have occured earlier.)
Now, what has this to do with likening Japan to Iowa? The gadget caught a fancy of a couple of Japanese teachers who went away and brought along more colleagues. After a few iterations they formed quite an admiring crowd willing to purchase the attraction. There was a problem though. The good businessman did not count on retail activity. All he had with him was a single gadget brought for demonstration purposes. This did not deter the crowd. They formed a line and one after another traded money and a business card for a promise of the gadget in the mail in a couple of weeks' time. No receipts were offered. Having served the last customer in this manner, Chaim expressed his appreciation of the Japanese market. On my part, I had a recollection of the "Out-of-towners" movie. (Adventures of a hapless Iowa couple in the New York city.) Is that how the Japanese might feel visiting in New York?
Igor Fedorovoch Sharygin passed away on March 12, 2004. He was a great geometer and pedagogue and a concerned citizen. Some of his untranslated articles concerning math education are available online.
|Contact| |Front page| |Contents| |CTK|
Copyright © 1996-2018 Alexander Bogomolny
73579757
