 |
Cut The Knot!by Alex Bogomolny |
Et tu ...
April 2003
![]()
|
'You do not know me yet,' Lieutenant Dub shouted again. 'You may perhaps know me from the good side, but wait till you know me from the bad side.' Jaroslav Hasek |
Much falls under the caption of Mathematics and Art, this year's theme of Mathematics Awareness Month.
Of all the fine arts, music may be the closest to mathematics, especially in its reliance on an abstract language. A competent performer can read music [Devlin, p. 4] right off a score sheet (which, please note, is not music in itself.) Likewise, a mathematician can read mathematics off a page of mathematical symbolism (which, too, is not mathematics in itself.) Unlike music, which is enjoyed by crowds that do not read the musical score, mathematics is rather misunderstood and even feared by masses not conversant with the mathematical language. The purpose of the Mathematics Awareness Month that is held each April by the Joint Policy Board for Mathematics is "to increase the visibility of mathematics as a field of study and to communicate the power and intrigue in mathematics to a larger audience."
In the 6th century B.C. Pythagoras observed that simple ratios of lengths of strings determine consonant musical intervals [Newman, p. 2183]. The 4th century B.C. student of Aristotle, Aristoxenus of Tarentum (364-304 B.C.), left us two treatises, Elements of Rhythm and Elements of Harmony. Aristoxenus divided the tetrachord into 30 parts, of which, in his diatonic syntonon, each tone has 12 parts, each semitone 6.
Accordingly, researchers attribute to Aristoxenus also the development of the widely used equal-tempered scale, but it were [Kline, p. 301] J. S. Bach and his son, Karl Philipp Emanuel, who established the scale as a fixture of modern Western music. (Bradley Lehman of the University of Michigan questions the prevalent view point. In two articles Bach's extraodinary temperament: our Rosetta Stone - 1, 2, Early Music.2005; 33: 1-22 and Early Music.2005; 33: 211-232, with plenty of mathematics and a flare for historical research, Lehman decodes Bach's diagram that heretofore was judged to be an intricate doodle as an instruction for tuning up musical instruments in an exquisite unequal temperament.) In that scale, an octave consists of twelve semitones, and the ratio of the frequencies of the starting notes of two consecutive octaves is exactly 2. The length of each interval between successive tones is the same, whereas the ratio of frequencies of successive notes is fixed and equals 21/12 [Stewart, ch 15, The Well-Tempered Calculator, Schroeder, p. 101, Newman, p. 2278-2314]. Exact ratios that were the Pythagorean choice, may only be approximated within the equal temperament: 3/2 as 1.498..., 4/3 as 1.335..., and so on. It is said that even such small discrepancies, known [Schroeder, p. 101] as the Pythagorean commas, could be detected by a good ear. The scale constrains a pianist, but less so a singer or a violinist thus inviting individual artistic treatment amidst mathematically imposed constraints. An additional advantage is the ability to start a composition at any note. In other words, the same composition could be translated to be played in any key.
In fact, the role of mathematics in music extends to composition itself. Masters such as Bach and Schoenberg have constructed and advocated vast mathematical theories for the composition of music [Kline, p. 134]. The rules for composition of canons and fugues have been described by D. Hofstadter in the first chapter of his now classic Gödel, Escher, Bach.
Music composition provides a fruitful field for experimentation. For example [Gardner, chapter on Fractal Music], Sergei Prokofiev composed some of the music for Sergei Eisenstein's 1938 film Alexander Nevsky in a peculiar manner. "Eisenstein provided Prokofiev with still shots of individual scenes of the movie as it was being filmed. Prokofiev then took these scenes and used the silhouette of the landscape and human figures as a pattern for the composition of the notes on the staff. He then orchestrated around these notes."
In the same book [Gardner, chapter Melody-Making Machines], M. Gardner gives further historical details on mechanization and mathematization of musical composition. In 1940, Heitor Villa-Lobos used Joseph Schillinger's mathematical system of composition to translate a New York City's skyline into piano music. Harold Jacobs made use of this example to enliven one of the exercises in his Elementary Algebra [Jacobs, p. 83]. Does the New York City's skyline define a function? If not, why?
Where there is music, there is mathematics. What's now the Avery Fisher Hall at the Lincoln Center for Performing Arts in New York City took originally a lot of verbal abuse due to poor acoustic performance. As it were, mathematics played a major role in detecting and rectifying the cause -- the poor scaling of the overhead acoustic panels that weakly reflected low-frequency sound (cello) components [Schroeder, p. 74]. The Avery Fisher Hall is now being booked as one of the best places in New York to observe classical music. This is yet another example of the public unknowingly enjoying the fruits and the power of mathematics.
There are additional points of contact between mathematics and music. For example, the chapter The Group-Theorist of Notre Dame in [Stewart, ch 13] puts bell tolling in a combinatorial framework. Fractal music is a source of several paradoxical curiosities [Schroeder, p. 96-97]. If converted to music and played at twice the recording speed, the everywhere continuous, but nowhere differentiable Weierstrass function would sound a semitone lower, instead of an octave higher, as one would expect.
Mathematics of course relates to other arts as well. In fact the thrust of the official MAM announcement is towards the visual arts:
The connection between mathematics and art goes back thousands of years. The ancient Greeks and Romans used mathematics in sculptures and to aesthetically design buildings. In the 15th century Leonardo da Vinci wrote "Let no one read me who is not a mathematician." In the 16th century Dürer employed mathematics to introduce perspective in drawings. In the 18th and 19th centuries mathematics was extensively used in the design of Gothic cathedrals, Rose windows, mosaics and tilings. In the 20th century geometric forms were fundamental to the cubists and many abstract expressionists. In recent decades several award winning sculptors have used topology as the basis for their pieces. The close connection between mathematics and art is most readily seen in the works of the Dutch artist M. C. Escher. Among the mathematical ideas represented in his work are: infinity, Möbius bands, tessellations, deformations, reflections, Platonic solids, spirals, symmetry, and the hyperbolic plane.
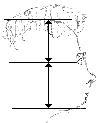
Both Leonardo da Vinci and Albrecht Dürer studied proportions of the human body and other objects. Paying attention to such proportions is bound to improve one's drawing ability in a very short order. It comes as a surprise to many [Edwards] that eyes are located midway on the skull. Children and most of adults draw them way too high. Ears are usually bigger than one thinks. The line of the eyes is perpendicular to the skull's central axis, even when the head is inclined. The tip of the nose is normally less than half way from the eye line to the chin, but more than a third. The center line of the mouth is about one third from the chin to the nose. The distance between the eyes is equal to the width of an eye. The corner of the eye, the lowest point of the chin and the far edge of the ear form an isosceles right triangle. Often the tip of the nose, the upper lip (and sometimes also the lower lip) and the chin lie on a straight line. Etc.
Some of the rules are illustrated below:
 |
 |
 |
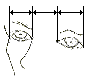 |
| The tip of the nose, the upper lip and the chin lie on a straight line. | The eyes are located midway on the skull. | The corner of the eye, the lowest point of the chin and the far edge of the ear form an isosceles right triangle. | The distance between the eyes is equal to the width of an eye. |
When drawing a portrait it's also important to remember that the human face is only approximately symmetric [Seckel, #85], such that attention must be paid equally to both sides of a portrait.
Perspective so dear to Dürer is endemic to our visual mechanism. When a drawing conflicts with the perspective expectations, human perception becomes confused. Perspective is thus a rich source of visual illusions. The Necker cube, i.e. a cube drawn in orthographic projection, lacks perspective clues, so that the eye has a difficulty choosing one possible interpretation at the expense of the other.
The same object placed "farther away" on a perspective drawing appears to grow in size [Mind's Eye, p. 91-92, Seckel, #87]. (In the applet below move scrollbars to modify the drawing attributes and drag the two shapes to locations of your choice. See when the effect is most pronounced.)
The brain uses other clues to interpret the retinal image. Take for example shadows that are thrown by opaque bodies. The distance between a body and its shadow provides an indication of the height of the body's location. Thus, with the shadow away from a body, the body appears to bounce up [Seckel, #13]:
Several write-ups on further relations of mathematics and visual arts could be found at the Math Forum site.
![]()
|
Who will wish to paint you, when no one wishes to see you? Gotthold Ephraim Lessing |
Let's have a second look at the MAM enterprise and, in particular, this year's theme selection. As I mentioned above, the idea behind the MAM is "to increase the visibility of mathematics as a field of study and to communicate the power and intrigue in mathematics to a larger audience." Should not the field of study which is mathematics be first defined or at least outlined to have a chance of being visible? Not necessarily, and not always. One can get an idea by juxtaposition. Take for example past MAM themes. Not once there is a doubt of what mathematics is not.
Mathematics and Decision Making (1996). Democracy is a human invention. Vote counting and power indices are mathematics. He who loves number counting is bound to be a mathematician. Democracy is one thing. The impossibility to satisfy everyone's political preferences is a proven mathematical truth.
Mathematics and the Internet (1997). First engineers invented the ethernet, then the internet. Computer scientists then came up with the web and eventually a browser. Mathematicians made the internet secure with very very big prime numbers.
Mathematics and Imaging (1998). Well, getting an image is imaging. Multiresolution image compression is mathematics. Just think of the abstraction of an expanding hierarchy of vector spaces and their wavelet bases. Incomprehensible abstractions is what mathematicians are good at. But even very abstract mathematical ideas may have practical applications.
Mathematics and Biology (1999). Even without a definition everything is very clear: epidemics is in domain of biology, epidemics modelling is in the purview of mathematics as is the solution of the resulting equations. This is what mathematicians do after all -- solving equations. Biology is biology. Mathematics is something else.
...
Mathematics and Art (2003). There are plenty of connections. Mathematics often engenders and even inspires art. Which is fine. But, by juxtaposition, or by inductive reasoning, if you will, art is art, whereas mathematics is something else.
I am sure that the message that mathematics is not art was not the intended purpose of the MAM/2003. No, of course, not. Mathematics is multifaceted, and its artistic nature is hard to deny. In a well-known book [p. 362], Kasner and Newman wrote:
Mathematics is an activity governed by the same rules imposed upon the symphonies of Beethoven, the paintings of Da Vinci, and the poetry of Homer.
J. W. H. Sullivan concurred [Schaaf, p. 12, Newman, p. 2021]:
The significance of mathematics resides precisely in the fact that it is an art; by informing us of the nature of our own minds it informs us of much that depends on our minds.
In the Middle Ages mathematics constituted a major part of the Liberal Arts. This is why math departments usually belong to Liberal Arts colleges. To be sure, mathematics has fundamentally changed since [Fadiman, p. 65]:
"Mathematics!" the devil exclaimed, horrified. "Do you think I've had time to waste learning such stuff? I've studied the Trivium and Quadrivium, but as for algebra -- say," he added resentfully, "what kind of a question is that to ask me?"
Indeed algebra and later branches of mathematics have not been originally included into the Liberal Arts curriculum. Naturally. Mathematics grew and developed considerably since the Middle Ages. But it became more of an art, not less.
I therefore feel apprehensive that the intention of the theme "Mathematics and Art" may be misconstrued. Indeed, I think it is highly probable that it will. "Sculpture and Art" or "Music and Art" look and sound incongruous, right? Why does not "Mathematics and Art"? I would be more comfortable with the caption "Mathematics and the Visual Arts" that was probably the intention to start with. However, I would remain apprehensive even if the latter were selected as the MAM theme.
Why? Because art is an active pursuit of beauty. The concept of beauty, however, and the expressive means of achieving it differ between various arts. G. E. Lessing (1729-1781) whose Laocoön: An Essay on the Limits of Painting and Poetry is considered the origin of modern esthetics, alluded in passing to a difference between painting and sculpture, the most congenial of any two arts:
The mere wide opening of the mouth -- apart from the fact that the other parts of the face are thereby violently and unpleasantly distorted -- is a blot in painting and a fault in sculpture which has the most untoward effect possible.
The Mandelbrot set is beautiful even if it is the monochromatic blot in the middle of the colorful depiction of equipotential lines. Just to think of the infinite intricacy of its whirl patterns which is produced by a mere quadratic formula takes one's breath away. Add to that the fact that the set serves as an index into the variety of Julia sets which, in turn, are classified according to the location of a single parameter inside the Mandelbrot set.
Certainly, the now common colorful pictures of the Mandelbrot set have great visual appeal. But then it is so much easier to substitute one for the other: "Ah, this is beautiful; and there's mathematics behind all that! Hence mathematics is beautiful!" I believe such misrepresentations are popular and deplore the disservice they might be doing to mathematics education. Here's an episode from my personal experience.
The incident occurred several years ago, when my older son took Geometry I in junior high. The boy was given an assignment. The basic idea was to take two line segments and divide them both into an equal number of subintervals. The division points then had to be connected to form a pretty web of straight lines. It was left to the student's imagination to combine the webs into more intricate patterns. The assignment did not follow, nor was preceded by any discussion of mathematical relevance. Division of a line segment into a number of equal parts with straightedge and compass -- no. The standard ruler with tick marks was sufficient to complete the assignment. The idea of an envelope of a family of lines had not been mentioned either. The assignment lacked any mathematical content whatsoever. I suggested to the boy to help him program QuickBasic to automatically generate various patterns. The boy insisted that programming was strictly and specifically forbidden. The assignment had to be completed by hand.
After a couple of unsuccessful attempts to engage the teacher, I was granted a meeting with the principal. In the school, the web patterns were proudly decorating all the available wall space. There were lace masterpieces by girls and intricate woodwork by boys -- all for the sake of extra credit. The assignment appeared to be a yearly milestone for Geometry I.
The principal readily admitted the shallowness of this exercise. The district math supervisor who was also present remained unmoved. After a short exchange I left utterly disappointed. What a waste of time! And zero knowledge acquisition. As far as I know, the assignment is still being offered as a mathematical attraction.
I am not building a critical edifice based on a single personal experience. There is definitely an unfortunate trend in mathematics education that seeks to endear mathematics on students with no attempt at transferring any significant mathematics. D. Hofstadter asks this question [Pritchard, p. xvii]:
Why does mathematics today have to be 'relevant' and 'fun', have to prove its worth by chewing gum like a sports star, acting sexy like a movie star, spouting cutesy sound-bytes like a with-it journalist, displaying itself as eye candy like a top model - but, heaven forbid, not by exploring unsuspected symmetries and subtle patterns purely for their own sake, like a scientist (let alone a mathematician!)?
The list of themes of Mathematics Awareness Week/Month bears witness:
- 1986 - Mathematics - The Foundation Discipline
- 1987 - The Beauty and Challenge of Mathematics
- 1988 - 100 Years of American Mathematics
- 1989 - Discovering Patterns
- 1990 - Communicating Mathematics
- 1991 - Mathematics - IT'S Fundamental
- 1992 - Mathematics and the Environment
- 1993 - Mathematics and Manufacturing
- 1994 - Mathematics and Medicine
- 1995 - Mathematics and Symmetry
- 1996 - Mathematics and Decision Making
- 1997 - Mathematics and the Internet
- 1998 - Mathematics and Imaging
- 1999 - Mathematics and Biology
- 2000 - Math Spans All Dimensions
- 2001 - Mathematics and the Ocean
- 2002 - Mathematics and the Genome
- 2003 - Mathematics and Art
The trend is undeniable: from The Beauty of Mathematics to its applications to the ambiguity of Mathematics and Art. Given that the applicability of mathematics is talked about all the year round, would it not make more sense to emphasize its beauty at least once a year, during this special event -- the Mathematics Awareness Month?
Branko Grünbaum wondered [Grünbaum, p. 53]:
... it is very likely that Escher did not wish to learn any of the mathematics we think might have helped him, and that we are much richer for it.
No one knows better than mathematicians themselves where the real beauty of mathematics lies. I believe it would enrich both mathematics education and public awareness of mathematical beauty were it pursued regularly and consistently. The other arts could take care of themselves.
References
- B. Edwards, The New Drawing on the Right Side of the Brain, Jeremy P. Tarcher, 1999
- K. Devlin, Mathematics: The Science of Patterns, Scientific American Library, 1997
- C. Fadiman, Fantasia Mathematica, Copernicus, 1997
- M. Gardner, The Colossal Book of Mathematics, W. W. Norton & Co, 2001
- B. Grünbaum, Mathematical Challenges in Escher's Geometry, M. C. Escher: Art and Science, edited by H. S. M. Coxeter, M. Emmer, R. Penrose and M. L. Teuber, North-Holland, 1986, pp 53-67
- J. Hasek, The Good Soldier Svejk, Viking Press, 1990
- D. Hofstadter, Gödel, Escher, Bach: An Eternal Golden Braid, Basic Books, 1999
- H. R. Jacobs, Elementary Algebra, W. H. Freeman and Co, 1979
- I. Kasner, J. Newman, Mathematics and the Imagination, Dover, 2001
- M. Kline, Mathematics in Western Culture, Oxford University Press, 1965
- G. E. Lessing, Laocoön: An Essay on the Limits of Painting and Poetry, Johns Hopkins Univ Press, Reprint edition, 1984
- Mathematics: Our Great Heritage, edited by W. L. Schaaf, Harper & Brothers, 1948
- M. Schroeder, Fractals, Chaos, Power Laws, W. H. Freeman and Co, 1991
- A. Seckel, The Art of Optical Illusions, Carlton Books, 2000
- A. Seckel, More Optical Illusions, Carlton Books, 2002
- I. Stewart, Another Fine Math You've Got Me Into ..., F. H. Freeman and Company, 1992
- The Changing Shape of Geometry, edited by C. Pritchard, Cambridge University Press, 2003
- The Mind's Eye, Readings from SCIENTIFIC AMERICAN, W. H. Freeman and Company, 1986
- The World of Mathematics, edited by J. Newman, Simon & Schuster Books, 2001
![]()
A Short Glossary of Terms
diatonic - not involving the sharpening or flattening of the notes of the major or minor scale nor the use of such notes as modified by accidentals (Diatonic Scales)
quadrivium - The collective name for the upper four liberal arts: arithmetic, music, geometry, and astronomy.
syntonic - emotionally in harmony with one's environment
tetrachord - any of several groups of four notes in descending order, in which the first and last notes form a perfect fourth
trivium - lower division of the seven liberal arts in medieval schools, consisting of grammar, logic, and rhetoric
![]()
|Contact| |Front page| |Contents|
Copyright © 1996-2018 Alexander Bogomolny
73385229
