A Property of Cyclic Quadrilateral

Here's a problem by Dao Thanh Oai posted by Co Gang Len at the CutTheKnotMath facebook page:

$ABCD$ is a cyclic quadrilateral. $E=AB\cap CD,$ $F=AD\cap BC.$

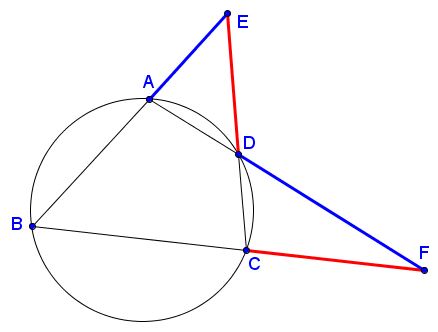
A Property of Cyclic Quadrilateral- problem

Prove that $AE\cdot DF = DE\cdot CF.$

Since $ABCD$ is cyclic, $\angle DAE=\angle BCD,$ so that $\sin\angle DAE = \sin\angle DCF.$

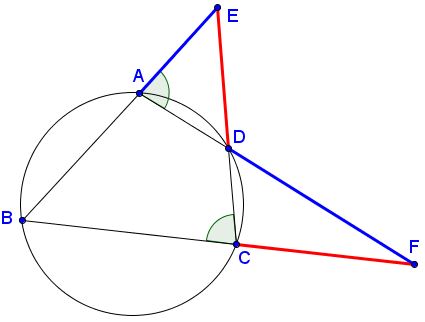
A Property of Cyclic Quadrilateral- solution

Now, applying the Sine Law,

$\displaystyle\frac{AE}{DE}=\frac{\sin\angle ADE}{\sin\angle DAE}=\frac{\sin\angle CDF}{\sin\angle DCF}=\frac{CF}{DF}$

which is the required identity.

72202692