Sum of Absolute Values

$\begin{align} f(x)=|x|&+2|x-1|+|x-2|+|x-4|\\ &+|x-6|+2|x-10|. \end{align}$

Find the minimum value of $f(x),$ for $x\in\mathbb{R}.$

$f(x)$ is the sum of functions with $V$-shaped graphs. The minimum is bound to occur at one of the "break" points. There are only six of them: $x=0,1,2,4,6,10.$ Let's check:

$\begin{align} f(0)&=0+2+2+4+6+20=34\\ f(1)&=1+0+1+3+5+18=28\\ f(2)&=2+2+0+2+4+16=26\\ f(4)&=4+6+2+0+2+12=26\\ f(6)&=6+10+4+2+0+8=30\\ f(10)&=10+18+8+6+4+0=46 \end{align}$

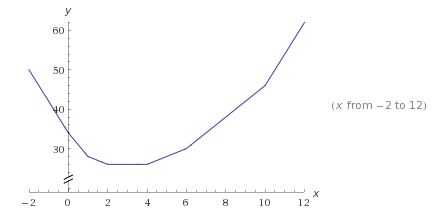
The minimum is achieved at two points, $x=2$ and $x=4$ and is equal to $26.$

Function $f$ being the sum of functions with $V$-shaped graph is piecewise linear. It is linear between any two successive breakpoints and outside the smallest interval that contains all of them, $[0,10]$ in this problem. So the fact that the minimum is achieved at two points, means that on the interval $[2,4]$ the function is constant. Indeed, here is its graph:

Now, is there anything about this problem that suggests a more insightful approach? There is indeed. A similar problem has been popularized by Paul J. Nahin:

The crucial insight is already apparent in the simplest graph of that sort, say, that of $g(x)=|x-1|+|x-2|:$

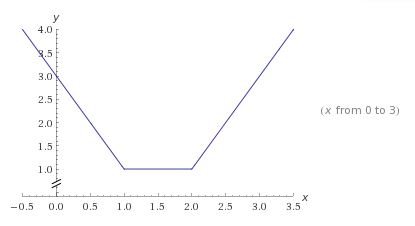
Any function $g(x)=|x-a|+|x-b|$ is constant in the interval $[a,b]$ (assuming $a\lt b)$ where it takes the value of $b-a.$ This is how it help to solve our problem: the given function is the sum of the simple ones (each of only two terms):

|x|+2|x-1|+|x-2|+|x-4|+|x-6|+2|x-10|

$\begin{align} f(x)&=|x|+|x-10|\\ &+|x-1|+|x-10|\\ &+|x-1|+|x-6|\\ &+|x-2|+|x-4|. \end{align}$

The first of these is constant on the interval $[0,10],$ the others, successively, on $[1,10],$ $[1,6],$ $[2,4],$ the last of which is common to all the pairs. We may even generalize.

Given an increasing sequence of real numbers $a_{1}\lt a_{2}\lt a_{3}\lt\ldots\lt a_{n}$ and a sequence of as many positive real coefficients $\{\alpha _{i}\},$ $i=1,2,\ldots ,n.$ Function $\displaystyle f(x)=\sum_{i=1}^{n}\alpha_{i}|x-a_{i}|$ achieves its minimum at one of the intervals $[a_{k},a_{k+1}]$ if and only if the coefficients $\{\alpha _{i}\}$ can be split into two groups with equal sums. Otherwise, the minimum is achieved at one of the given points $\{a_{i}\}.$

Proof

The proof is by induction.

The claim is obvious when there are just one or two terms.

For a larger $n,$ assume without loss of generality that $\alpha _{1}\le\alpha _{2}.$ Then,

$\begin{align} f(x)&=\bigg[\alpha _{1}|x-a_{1}|+|x-a_{n}|\bigg] \\ &\space\space +\bigg[\alpha _{2}|x-a_{2}|+\ldots +\alpha _{n-1}|x-a_{n-1}|+(\alpha _{n}-\alpha_{1})|x-a_{n}|\bigg], \end{align}$

where the function in brackets has fewer than $n$ break points. Also, the coefficients $\alpha_{2},\ldots,\alpha_{n-1},\alpha_{n}-\alpha_{1}$ could be split into two groups of equal sums only if that is true of the original $n$ coefficients. To complete the induction, it suffices to observe that the interval $[a_{1},a_{n}]$ where the first term is constant, contains all the break points of the second term.

Given an increasing sequence of real numbers $a_{1}\lt a_{2}\lt a_{3}\lt\ldots\lt a_{n}.$ Find the minimum of function $\displaystyle f(x)=\sum_{i=1}^{n}(x-a_{i})^{2}.$

Solution

Notice that

$\begin{align} f(x)-f(y)&=\sum_{i=1}^{n}\bigg[(x-a_{i})^{2}-(y-a_{i})^{2}\bigg]\\ &=\sum_{i=1}^{n}\bigg[(x^{2}-y^{2})-2(x-y)a_{i}\bigg]\\ &=n(x^{2}-y^{2})-2(x-y)\sum_{i=1}^{n}a_{i}. \end{align}$

Letting $\displaystyle y_{0}=\frac{a_{1}+\ldots+a_{n}}{n}$ gives

$\begin{align} f(x)-f(y_{0})&=n(x^{2}-y_{0}^{2})-2(x-y_{0})\sum_{i=1}^{n}a_{i}\\ &=n(x^{2}-y_{0}^{2})-2nxy_{0}+2ny_{0}^{2}\\ &=n(x^{2}-2xy_{0}+y_{0}^{2})=n(x-y_{0})^{2}\ge 0, \end{align}$

implying that the minimum is achieved at $\displaystyle y=\frac{a_{1}+\ldots+a_{n}}{n}.$

Is there a further modification/generalization?

The example came from an excellent book by Xu Jiagu, Lecture Notes on Mathematical Olympiad Courses, v 8, (For senior section, v 1), World Scientific, 2012, p.54