Telescoping Squares

The following problem has been posted by Kunihiko Chikaya at the Short Mathematical Idea facebook group.

Prove that

$\displaystyle 2^{2013}\cos ^{4026}\bigg(\frac{1}{2}\bigg)\cos ^{4025}\bigg(\frac{1}{3}\bigg)\cos ^{4024}\bigg(\frac{1}{4}\bigg)\cdots\cos \bigg(\frac{1}{4027}\bigg)\gt\sqrt{2014}.$

Practically identical solutions have been submitted by Leo Giugiuc and Siddig Awad Siddig. After an initial step, the problem reduces to a telescoping product.

The basic step is the observation known from the beginning calculus that, for all real $x,$ $\displaystyle\cos x\ge 1-\frac{x^{2}}{2},$ with equality only at $x=0.$ On the other hand, for the double argument, $\cos 2x=2\cos ^{2}x-1,$ implying that

$\displaystyle\cos ^{2}x=\frac{1}{2}(1+\cos 2x)\gt\frac{1}{2}(1+1-\frac{(2x)^{2}}{2})=1-x^2.$

Here's a graphic illustration:

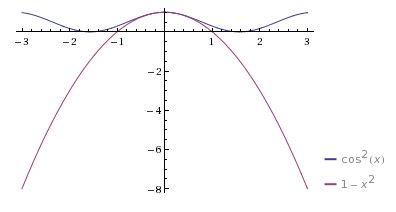
$(cos(x))^2\gt 1-x^2$

Thus we have in shorthand notations:

$\displaystyle \prod_{k=2}^{4027}\cos^{2} \bigg(\frac{1}{k}\bigg)^{4028-k}\gt \prod_{k=2}^{4027}\bigg(1-\frac{1}{k^2}\bigg)^{4028-k},$

so that the problem will be solved if we manage to prove a stronger inequality:

$\displaystyle 2^{4026}\prod_{k=2}^{4027}\bigg(1-\frac{1}{k^2}\bigg)^{4028-k}\gt 2014.$

Let's do that:

$\begin{align}\displaystyle 2^{4026}\prod_{k=2}^{4027}\bigg(1-\frac{1}{k^2}\bigg)^{4028-k}&=2^{4026}\prod_{k=2}^{4027}\bigg(\frac{k^{2}-1}{k^2}\bigg)^{4028-k}\\ &=2^{4026}\prod_{k=2}^{4027}\bigg(\frac{(k-1)(k+1)}{k^2}\bigg)^{4028-k}\\ &=2^{4026}\frac{\displaystyle\prod_{k=2}^{4027}(k-1)^{4028-k}\prod_{k=2}^{4027}(k+1)^{4028-k}}{\displaystyle\prod_{k=2}^{4027}k^{2(4028-k)}}\\ &=2^{4026}\frac{\displaystyle\prod_{k=1}^{4026}k^{4027-k}\prod_{k=3}^{4028}k^{4029-k}}{\displaystyle\prod_{k=2}^{4027}k^{2(4028-k)}}\\ &=2^{4026}\frac{2^{4025}}{2^{2\cdot 4026}}\cdot\frac{4028}{1}=2014, \end{align}$

as required.

Note: there is a whole page of telescoping examples.

71869101