The Rascal Triangle

You are to fill the next row in the triangular array:

				1
			1		1
		1		2		1
	1		3		3		1
?		?		?		?		?

You would not be alone to thinnk that the correct answer is, or rather was expected to be, the next row of the Pascal triangle, viz.,

1   4   6   4   1

After all, the question was included in an I.Q. test. However, the three authors of an article in the latest College Mathematics Journal, not only observed that the problem, as stated, could be satisfied by any 5-tuple of integers, but found in some sense a natural answer radically different from the expected.

Probably grudgingly, the authors allowed for extremal 1s, like in the Pascal triangle, but to compute other entries they devised an entirely different procedure. Here is a part of the configuration of four numbers in the number triangle that form a rhombus:

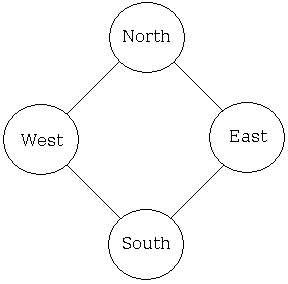
In the Pascal triangle the number denoted South is calculated as South = West + East. The article suggets an alternative:

South = (West × East + 1) / North.

which, for the problem at hand, produced a different row:

1   4   5   4   1

They also found the next row according to their prescription:

1   5   7   7   5   1

and the next

1   6   9   10   9   6   1

Wonderfully, even though the division was involved on every step, the rows come out to consist of integers.

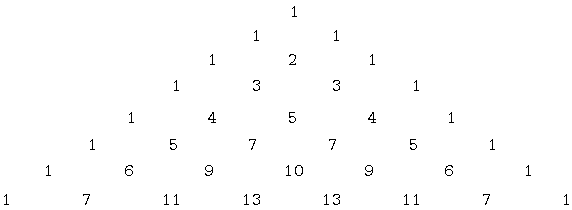
To prove that this is always so, introduce a system of coordinates (m, n) in the triangle, where m designates the m^th NE-SW diagonal (starting with 0), while n designates the n^th term (again starting with 0) on the diagonal. So the first, i.e., the 0^th diagonal consists of 1s: 1 1 1 1 .... Let's combine the first few diagonals in a table:

0: 1   1   1   1   1   1 ...
1: 1   2   3   4   5   6 ...
2: 1   3   5   7   9  11 ...
3: 1   4   7  10  13 16 ...
4: 1   5   9  13  17 20 ...

The pattern is rather obvious: the m^th diagonal goes 1, m+1, 2m+1, ..., nm+1. In our coordinate system the term with coordinates m and n is simply nm + 1. Let's check formally that this is indeed so. The terms involved in the computations are

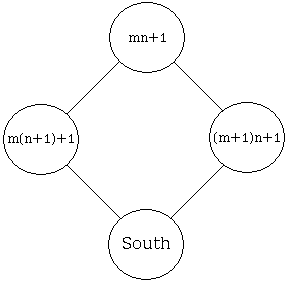
West × East + 1	= [m(n + 1) + 1][(m + 1)n + 1] + 1
	= [m(n + 1) + 1][(m + 1)n + 1] + 1
	= [(mn + 1) + m][(mn + 1) + n] + 1
	= (mn + 1)(mn + 1) + m(mn + 1) + (mn + 1)n + mn + 1
	= (mn + 1)[(mn + 1) + m + n + 1]
	= (mn + 1)[(mn + 1) + m + n + 1]
	= (mn + 1)[(m + 1)(n + 1) + 1]

It follows that the formula South = (West × East + 1) / North leads to

South = (m + 1)(n + 1) + 1,

which, as expected, corresponds to the pair (m + 1, n + 1). Thus the algorithm indeed generates a triangle of integers.

The entries in the triangle, if listed sequencially, appear in the Encyclopedia of Integer Sequences. The algorithm is the same as used by J. Conway and R. Guy to generate numeric Frieze patterns.

References

1. Alif Anggoro, Eddy Liu, and Angus Tulloch, The Rascal Triangle, The College Mathematics Journal, V. 41, N. 5, November 2010, pp. 393-395
2. J. H. Conway and H. S. M. Coxeter,Triangulated polygons and frieze patterns, THE MATHEMATICAL GAZETTE, v 57 (1973) 87-94, 175-183
3. J. H. Conway and R. K. Guy, The Book of Numbers, Springer-Verlag, NY, 1996.
4. H. S. M. Coxeter, J. F. Rigby, Frieze Patterns, Triangulated Polygons and Dichromatic Symmetry, in The Lighter Side of Mathematics, R. K. Guy and E. Woodrow (eds.), John Wiley & Sons, NY, 1961

• Step into the Elliptic Realm
• Simple Somos Sequence - a Russian Olympiad problem
  • Simple Somos Sequence Calculator
• The Rascal Triangle
• Frieze Patterns

|Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny