Parabola and Abutting Equilateral Triangles
An engaging problem has been proposed by Norman Anning (AMM, 1992, p.92) and solved by G. W. Smith. The problem has been included in R. Honsberger's collection Mathematical Morsels (MAA, New Math Library, 1978), #64.
Equilateral triangles of sides $1,$ $3,$ $5,$ $\ldots,$ $2n-1,$ $\ldots,$ are placed end-to-end along a straight line.
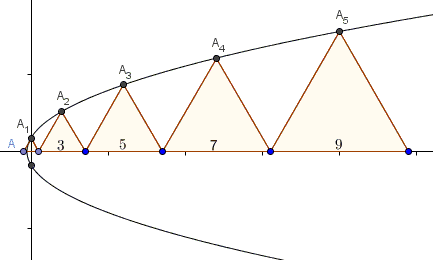
Show that the vertices which do not lie on the line all lie on a parabola and that their focal radii are all integers.
|Contact| |Front page| |Contents| |Algebra| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyEquilateral triangles of sides $1,$ $3,$ $5,$ $\ldots,$ $2n-1,$ $\ldots,$ are placed end-to-end along a straight line.

Show that the vertices which do not lie on the line all lie on a parabola and that their focal radii are all integers.
Solution
Let's draw the Cartesian coordinates so that the origin is at the midpoint of the base of the first triangle so that $A_1$ lies on the $y-$axis. The $x-$axis is the line where the triangles are located. $A_1$ is the point $(0,\sqrt{3}/2).$ Since the base of the $n$th triangle is $2n-1$ we can easily find the abscissa ($x-$coordinate) of $A_n:$
$\displaystyle x_{n}=\frac{1}{2}+3+5+\ldots+(2n-3)+\frac{2n-1}{2}=n(n-1).$
The ordinate ($y-$coordinate) of $A_n$ is $\displaystyle y_{n}=\frac{\sqrt{3}}{2}(2n-1).$ Expressing $n$ in terms of $y_n$ and substituting that into the formula for $x_n$ gives $4y_{n}^2=3(x_{n}-4).$ But $4y^2=3(x-4)$ is an equation of a parabola with the axis along the $x-$axis, vertex at $(-1/4,0)$ and focus at $(1/2,0).$ With this we now compute the focal radii:
$\displaystyle \sqrt{\bigg[n(n-1)-\frac{1}{2}\bigg]^{2}+\bigg[(2n-1)\frac{\sqrt{3}}{2}\bigg]^{2}}=n^2-n+1$
which is certainly an integer.
|Contact| |Front page| |Contents| |Algebra| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73571239
