Why sin(x)/x tends to 1

The following short note has appeared in a 1943 issue of the American Mathematical Monthly.

The proof of the fundamental theorem

(*)

$\displaystyle\lim_{\theta\rightarrow 0}\frac{\sin\theta}{\theta}=1$

as ordinarily given in elementary books, usually depends on two unproved theorems. The following proof is at least simpler, if not more rigorous.

If $P$ is the perimeter of a regular $n$-gon inscribed in a circle of radius $r,$ then $\displaystyle P=2nr\sin\frac{\pi}{n}$ and we know from plane geometry that $\displaystyle\lim_{n\rightarrow\infty}P=2\pi r.$ Hence $\displaystyle\lim_{n\rightarrow\infty}\bigg(\frac{n}{\pi}\bigg)\sin\frac{\pi}{n}=1$ and if we let $\displaystyle\frac{\pi}{n}=\theta$ then $\theta\rightarrow 0$ as $n\rightarrow\infty$ and conversely. Hence, $\displaystyle\lim_{\theta\rightarrow 0}\frac{\sin\theta}{\theta}=1.$

I do not exactly know how the limit has been ordinarily established more than 70 years ago, nor is it clear which two unproved theorems from plane geometry the note refers to. However, it is hard to miss the fact that the note may at best be furnishing motivation for the fact, but by no means prove it.

The note appears to follow this logic. Assume $\displaystyle\lim_{n\rightarrow\infty}x_{n}=a.$ Then $\displaystyle\lim_{n\rightarrow\infty}f(x_{n})=L$ implies $\displaystyle\lim_{x\rightarrow a}f(x)=L.$ This is patently false. Convergence of a function over a sequence around a point does not ensure convergence of a function, let alone existence of the limit at this point. Counterexamples are easy to construct. Consider, for example, function $\displaystyle f(x)=\sin\frac{1}{x}$ around $a=0$ and the sequence $\displaystyle x_{n}=\frac{1}{\pi n}.$ Obviously, $\displaystyle\lim_{x\rightarrow 0}f(x)$ does not exist, whereas $\displaystyle\lim_{n\rightarrow\infty}f(x_{n})=0.$

Personally, I find proof of (*) based on the Squeeze (or Squeezing) Theorem beautifully transparent and satisfactory.

Consider a unit circle (the circle of radius $1$) and small angle (arc) $\theta\gt 0.$

squeezed sine

Comparing the length of arcs and segments or the area of triangles and circular sectors in the diagram we concluded that $\sin\theta\lt\theta\lt\tan\theta.$ Division by $\sin\theta$ gives

$\displaystyle 1\lt\frac{\theta}{\sin\theta}\lt\frac{1}{\cos\theta}.$

Now passing to the reciprocals me obtain

$\displaystyle \cos\theta\lt\frac{\sin\theta}{\theta}\lt 1.$

Note that, even though we started with $\theta\gt 0,$ the latter inequality also holds for negative $\theta.$

Since, as we know, $\displaystyle\lim_{\theta\rightarrow 0}\cos\theta = 1,$ (*) follows immediately.

As a matter of motivation for (*), it is also possible to use areas of regular polygons, instead of their perimeters. The area of an $n$-gon inscribed into a unit circle equals $\displaystyle n\tan (\pi/n)=\pi\frac{\tan (\pi/n)}{\pi/n},$ and, since, $\displaystyle \cos\theta\lt\frac{\sin\theta}{\theta}\lt 1$ we again get the required $\displaystyle\lim_{\theta\rightarrow 0}\frac{\sin\theta}{\theta}=1.$

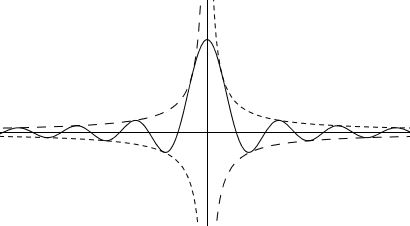
Finally, observe that the function $\displaystyle f(x)=\frac{\sin x}{x}$ is not a priori defined for $x=0.$ Having $\displaystyle\lim_{x\rightarrow 0}f(x)=1$ suggests setting $f(0)=1,$ which makes the function not only defined at $x=1$ but also continuous at this point. Here's the graph of $\displaystyle f(x)=\frac{\sin x}{x}$ "squeezed" between the graphs $y=\pm\displaystyle\frac{1}{x}.$

graph of sin(x)/x

Reference

M. S. Knebelman, An Elementary Limit, Am Math Monthly, v 50 (1943), p 507. Also included into Century of Calculus, v. 1, T. M. Apostol et al, MAA, 1992, p 113

71946909