Word problems that lead to simple linear equations, II

This is a continuation of the discussion on the word or story problems. The first task in solving word problems is to translate them into the language of mathematics: equations. Since an equation captures only essential details of a problem, the translation is not word-for-word. Inessential details must be left out.

(Note: In the applet below, all underlied words and numbers can be clicked on. In fact you can see some changes clicking anywhere in the applet area. Click, click, click ... and see what happens.)

// foreground color // background color // information pieces start with '@', followed by // a single letter from {v,a,f,e}, followed by ": ". // v - variable - anything that may change on a click // variables must precede all other pieces // f - formulation - word problem with embedded variables. // Many formulations are possible for a single problem. // Only one is shown at a time // e - equation - equation is like a formulation with a // potential provision to, e.g., enclose negative numbers // into parentheses // a - answer - like an equation, but allowed to have a parsable // portion. Parsables are written in the reverse Polish notations // with variables and operations separated by a comma // d - directive // define color, skip line // // whatever it is, a variable can be of the three types: // I = integer - on click changes up (right of center) and down (left of center) // a = attribute - any clickable and changeable word // v = variable - like an attribute but without related attributes // all 'name's below are 1 letter from [A-Ba-b0-9] // i, name, initial value, min, max // a, name, related attribute, list of values // v, name, list of symbols // formulations // equations // answers

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

This problem deals with two numbers (ages of boys, or girls, or unicorns - this is quite inessential.) One of the numbers is known, another is not. The key word in the problem is "times". One of the numbers at hand exceeds the second number by a given factor.

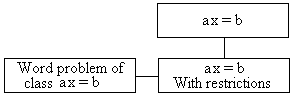
The problem at hand belongs to a class of problems described by the equation

(4)

ax = b,

where x is a variable that denotes the unknown, while a and b are constant (but arbitrary) coefficients.

Equation (4) says that two entities are (or expected to be) equal. One is the number on the right - b. The other (incidentally) a product of two numbers - ax. A quick solution to the equation is obtained following a rule similar to Euclid's

if equals be divided into equals, the results are equal.

Thus we are prompted to conclude that (ax)/a = b/a, or

(5)

x = b/a,

that apparently asserts that the unknown is actually equal to b/a. The problem is solved. Or is it?

Do not forget that in (4) coefficients a and b are arbitrary. As far as the equation (4) is concerned, they may be anything. Solving a general equation like (4) is different from solving specific equations like 4x = 12, whose solution is readily obtained as x = 12/4, x = 3. In (4) we are obligated to account for all possible specific cases. Most of the cases are, indeed, handled in the same manner, as in (5). The exception is when a = 0. This is one of characteristic properties of zero that multiplied by another number, any number, it does not change. We may not know x, but if a = 0, then ax is bound to be 0! So unless b is also zero, the equality in (4) is not possible. We arrive at the following cases:

a	b
Not zero	Any	x = b/a
Zero	Not zero	(4) has no solutions
Zero	Zero	any x solves (4)

The original problem imposes additional (semantic) constraints. First of all, no one's age can be 0 or negative. Secondly, you would probably be very much surprised to hear a reply "13.5" to a question of yours, "How old are you?" Somewhere in the grade school, where kids of about the same age learn, work, and play together, the difference of a few month loses its significance. From that time on, we count years of our life with integers, discarding the fractional part. This means that in the original word problem it is very natural to assume that all quantities involved are positive integers such that a divides b evenly. (However, this particular fact is not carved in stone. Faced with a similar problem, you may want to check with your teacher.) The same goes for the comon usage of the word times. We never say "1 time as young", let alone "1 times as young."

However, assume the problem reads

A 40 years old father is 7 times older than his son. What is the son's age?

The formal answer is 40/7 years. Which does not look quite right. For, one would never hear such year count in the context of age determination. Is there a better answer? There might. For example, rounding to the nearest integer, we may suggest that the son's age is 6. This will not mean that 6 = 40/7, but rather that in our opinion the boy is big enough to count his age by years without the fractional part or months. In situations like this, it's the context rather than mathematics that determines the expected answer.

To summarize, above we have looked into three classes of problems. One - that of solving an abstract equation ax = b - has a unique solution for a different from 0. When a = 0, the equation either has infinitely many solutions (b = 0), or no solutions at all (b different from 0). Problems of the second kind deal with solving the same equation ax = b but subject to some constraints. For example, we may be only interested in positive integer solutions. In which case, fractional solutions of the equation ax = b will not solve the restricted problem and thus must be discarded. The third kind of problems - certain word problems - when formalized, lead to problems ofof the second kind with constraints determined from the word problem context.

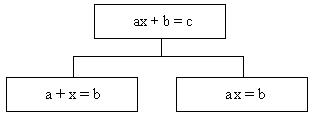
The names "a" and "b" for the constants in the equation (4) are as arbitrary as they were in the equation a + x = b and are as arbitrary as the name "x" for the unknown. The latter equation is verbalized as "a constant plus the unknown equals another constant", while (4) is expressed as "a constant times the unknown equals another constant". Bearing in mind the arbitrariness of the names given to constants, we combine two equations a + x = b and ax = b into one:

On the one hand, both a + x = b and ax = b are specializations of the equation ax + b = c. (The first is obtained from ax + b = c when a = 1, the second when b = 0.) On the other hand, both a + x = b and ax = b emerge as intermediate steps when solving a more general equation ax + b = c.

Think of the term ax as another unknown. ax + b = c is then a shorthand for "the (new) unknown plus a constant equals another constant" which is solved by subtracting the first constant from both sides. The result of this step is an equation like (4): "the unknown times a constant equals a constant". The latter is solved, as in (5), by dividing both sides by the same constant.

Word Problems

(There are many more word problems discussed and solved at this site.)

71950138